
【题目】某地区现有一个直角梯形水产养殖区ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在点P处有一灯塔(如图),且点P到BC,CD的距离都是1200m,现拟将养殖区ACD分成两块,经过灯塔P增加一道分隔网EF,在△AEF内试验养殖一种新的水产品,当△AEF的面积最小时,对原有水产品养殖的影响最小.设AE=d.
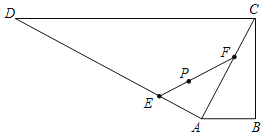
(1)若P是EF的中点,求d的值;
(2)求对原有水产品养殖的影响最小时的d的值,并求△AEF面积的最小值.
【答案】(1)480![]() ; (2)对原有水产品养殖的影响最小时,d=480
; (2)对原有水产品养殖的影响最小时,d=480![]() .△AEF面积的最小值为192000m2
.△AEF面积的最小值为192000m2
【解析】
(1)建立平面坐标系,求出直线AD,AC的方程,根据P为EF的中点列方程得出E点坐标,从而可计算d;
(2)根据基本不等式得出AEAF的最小值,进而求出△AEF的面积最小值.
解:(1)以A为坐标原点,AB所在直线为x轴,建立如图所示的平面直角坐标系,
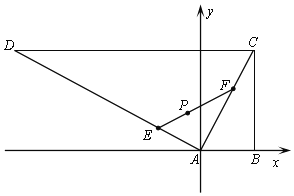
则C(800,1600),B(800,0),P(-400,400),D(-3200,1600).
AC所在直线方程为y=2x,AD所在直线方程为y=-![]() x.
x.
设E(-2m,m),F(n,2n),m>0,>0.
∵P是EF的中点,∴![]() ,解得
,解得![]() ,
,
∴E(-960,480),
∴d=|AE|=![]() =480
=480![]() .
.
(2)∵EF经过点P,∴kPE=kPF,
即![]() =
=![]() ,化简得80m+240n=mn.
,化简得80m+240n=mn.
由基本不等式得:mn=80m+240n≥160![]() ,
,
即mn≥76800,当且仅当m=3n=480时等号成立.
∵kACkAD=-1,∴AC⊥AD,
∴S△AEF=![]() AEAF=
AEAF=![]() m
m![]() n=
n=![]() mn≥
mn≥![]() 76800=192000,
76800=192000,
此时E(-960,480),d=AE=480![]() .
.
故对原有水产品养殖的影响最小时,d=480![]() .△AEF面积的最小值为192000m2.
.△AEF面积的最小值为192000m2.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ;
;
(1)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且当
,且当![]() ,
,![]() ,求
,求![]() 在
在![]() 上的解析式;
上的解析式;
(3)对于(2)中的![]() ,若关于
,若关于![]() 的不等式
的不等式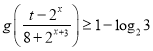 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 平面
平面![]() ,且四边形
,且四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(3)点![]() 是线段
是线段![]() 上的动点,当直线
上的动点,当直线![]() 与
与![]() 所成的角最小时,求线段
所成的角最小时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a>0),且f(1)![]() .
.
(1)求证:函数f(x)有两个不同的零点;
(2)设x1,x2是函数f(x)的两个不同的零点,求|x1﹣x2|的取值范围;
(3)求证:函数f(x)在区间(0,2)内至少有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 有两个不等的实数根,求
有两个不等的实数根,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知![]() ,且2an+1=an+1(n∈N*).
,且2an+1=an+1(n∈N*).
(1)求证:数列{an-1}是等比数列;
(2)若bn=nan,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴的正半轴于
轴的正半轴于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 方程为
方程为![]() (
(![]() ),且
),且![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 经过点
经过点![]() ,设
,设![]() 的斜率为
的斜率为![]() ,
,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
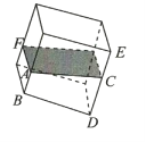
【题目】在一个长方体的容器中,里面装有少量的水,现在将容器绕着其底部的一条棱倾斜.
(1)在倾斜的过程中,水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)在倾斜的过程中,水的形状也不断变化,可以是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com