
 =-
=- .
.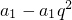 =3,再由q=-
=3,再由q=- 可得 a1=4,an =4
可得 a1=4,an =4 .
. )+3
)+3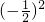 +…+n
+…+n ,
, Tn =4[(-
Tn =4[(- )+2
)+2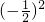 +3
+3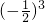 +…+n
+…+n  ],
], Tn =4[1+(-
Tn =4[1+(- )+
)+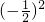 +
+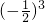 +…+
+…+ -n
-n  ],
], ×[
×[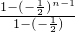 -n
-n ]=
]= ×[
×[ -
-
 n
n  ].
]. 的值.
的值. 可得a1的值,从而求出数列{an}的通项公式.
可得a1的值,从而求出数列{an}的通项公式. )+3
)+3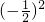 +…+n
+…+n ,用错位相减法求出前n项的和Tn 的值.
,用错位相减法求出前n项的和Tn 的值.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•蓝山县模拟)统计某校高三年级100名学生的数学月考成绩,得到样本频率分布直方图如下图所示,已知前4组的频数分别是等比数列{an}的前4项,后6组的频数分别是等差数列{bn}的前6项,
(2012•蓝山县模拟)统计某校高三年级100名学生的数学月考成绩,得到样本频率分布直方图如下图所示,已知前4组的频数分别是等比数列{an}的前4项,后6组的频数分别是等差数列{bn}的前6项,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com