
【题目】已知曲线y=Asin(ωx+φ)(A>0,ω>0)上的一个最高点的坐标为(![]() ,
,![]() ),由此点到相邻最低点间的曲线与x轴交于点(
),由此点到相邻最低点间的曲线与x轴交于点(![]() π,0),φ∈(﹣
π,0),φ∈(﹣![]() ,
,![]() ).
).
(1)求这条曲线的函数解析式;
(2)写出函数的单调区间.
【答案】(1)y=![]() sin(
sin(![]() x+
x+![]() );(2)[4kπ+
);(2)[4kπ+![]() ,4kπ+
,4kπ+![]() ],k∈Z.
],k∈Z.
【解析】解:(1)由题意可得A=![]() ,
,![]()
![]() =
=![]() ﹣
﹣![]() ,求得ω=
,求得ω=![]() .
.
再根据最高点的坐标为(![]() ,
,![]() ),可得
),可得![]() sin(
sin(![]() ×
×![]() +φ)=
+φ)=![]() ,即sin(
,即sin(![]() ×
×![]() +φ)=1 ①.
+φ)=1 ①.
再根据由此最高点到相邻最低点间的曲线与x轴交于点(![]() π,0),可得得
π,0),可得得![]() sin(
sin(![]() ×
×![]() +φ)=0,即sin(
+φ)=0,即sin(![]() +φ)=0 ②,
+φ)=0 ②,
由①②求得φ=![]() ,故曲线的解析式为y=
,故曲线的解析式为y=![]() sin(
sin(![]() x+
x+![]() ).
).
(2)对于函数y=![]() sin(
sin(![]() x+
x+![]() ),令2kπ﹣
),令2kπ﹣![]() ≤
≤![]() +
+![]() ≤2kπ+
≤2kπ+![]() ,求得4kπ﹣
,求得4kπ﹣![]() ≤x≤4kπ+
≤x≤4kπ+![]() ,
,
可得函数的增区间为[4kπ﹣![]() ,4kπ+
,4kπ+![]() ],k∈Z.
],k∈Z.
令2kπ+![]() ≤
≤![]() +
+![]() ≤2kπ+
≤2kπ+![]() ,求得4kπ+
,求得4kπ+![]() ≤x≤4kπ+
≤x≤4kπ+![]() ,
,
可得函数的减区间为[4kπ+![]() ,4kπ+
,4kπ+![]() ],k∈Z.
],k∈Z.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】有4个不同的球,4个不同的盒子,把球全部放入盒子内.
(1)共有几种放法?
(2)恰有1个空盒,有几种放法?
(3)恰有2个盒子不放球,有几种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】截止到1999年底,我国人口约为13亿,若今后能将人口平均增长率控制在1%,经过x年后,我国人口为y(单位:亿).
(1)求y与x的函数关系式y=f(x);
(2)求函数y=f(x)的定义域;
(3)判断函数f(x)是增函数还是减函数,并指出函数增减的实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张师傅想要一个如图1所示的钢筋支架的组合体,来到一家钢制品加工店定制,拿出自己画的组合体三视图(如图2所示).店老板看了三视图,报了最低价,张师傅觉得很便宜,当即甩下定金和三视图,约定第二天提货.第二天提货时,店老板一脸坏笑的捧出如图3–1所示的组合体,张师傅一看,脸都绿了:“奸商,怎能如此偷工减料”.店老板说,我是按你的三视图做的,要不我给你加一个正方体,但要加价,随机加上了一个正方体,得到如图3–2所示的组合体;张师傅脸还是绿的,店老板又加上一个正方体,组成了如图 3–3 所示的组合体,又加价;张师傅脸继续绿,店老板再加一个正方体,组成如图 3–4 所示的组合体,再次加价;双方就三视图争吵不休……
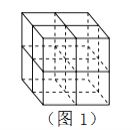
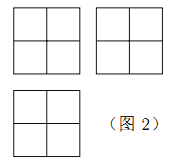
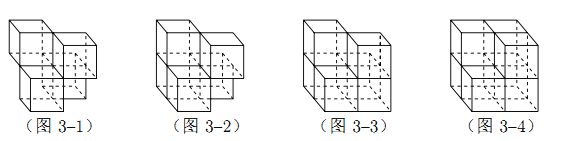
你认为店老板提供的![]() 个组合体的三视图与张师傅画的三视图一致的个数是( )
个组合体的三视图与张师傅画的三视图一致的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(16名女员工,14名男员工)的得分,如下表:
女 | 47 | 36 | 32 | 48 | 34 | 44 | 43 | 47 | 46 | 41 | 43 | 42 | 50 | 43 | 35 | 49 |
男 | 37 | 35 | 34 | 43 | 46 | 36 | 38 | 40 | 39 | 32 | 48 | 33 | 40 | 34 |
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 总计 | |
女 | 16 | ||
男 | 14 | ||
总计 | 30 |
(3)根据上述表中数据,利用独立性检验的方法判断,能否有99%的把握认为该企业员工“性别”与“工作是否满意”有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期内的图象时,列表并填入的数据如下表:
x |
| x1 |
| x2 | x3 |
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(1)求x1,x2,x3的值及函数f(x)的表达式;
(2)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,求函数y=f(x)·g(x)在区间![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王、小李两位同学玩掷骰子(骰子质地均匀)游戏,规则:小王先掷一枚骰子,向上的点数记为x;小李后掷一枚骰子,向上的点数记为y,
(1)在直角坐标系xOy中,以(x,y)为坐标的点共有几个?试求点(x,y)落在直线x+y=7上的概率;
(2)规定:若x+y≥10,则小王赢;若x+y≤4,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com