
【题目】甲、乙、丙3人站到共有6级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法总数是( )
A.90B.120C.210D.216
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
男生 | 女生 | |||
支持 | 不支持 | 支持 | 不支持 | |
方案一 | 200人 | 400人 | 300人 | 100人 |
方案二 | 350人 | 250人 | 150人 | 250人 |
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案的概率估计值记为![]() ,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为
,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为![]() ,试比较
,试比较![]() 与
与![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知焦点为![]() 的抛物线
的抛物线![]() 上有一动点
上有一动点![]() ,过点
,过点![]() 作抛物线的切线
作抛物线的切线![]() 交
交![]() 轴于点
轴于点![]() .
.
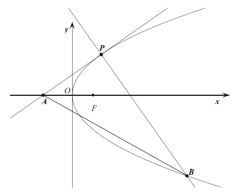
(1)判断线段![]() 的中垂线是否过定点,若是求出定点坐标,若不是说明理由;
的中垂线是否过定点,若是求出定点坐标,若不是说明理由;
(2)过点![]() 作
作![]() 的垂线交抛物线于另一点
的垂线交抛物线于另一点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
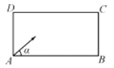
【题目】台球运动已有五、六百年的历史,参与者用球杆在台上击球.若和光线一样,台球在球台上碰到障碍物后也遵从反射定律如图,有一张长方形球台ABCD,![]() ,现从角落A沿角
,现从角落A沿角![]() 的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则
的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上一动点A的坐标为![]() .
.
(1)求点A的轨迹E的方程;
(2)点B在轨迹E上,且纵坐标为![]() .
.
(i)证明直线AB过定点,并求出定点坐标;
(ii)分别以A,B为圆心作与直线![]() 相切的圆,两圆公共弦的中点为H,在平面内是否存在定点P,使得
相切的圆,两圆公共弦的中点为H,在平面内是否存在定点P,使得![]() 为定值?若存在,求出点P坐标;若不存在,请说明理由.
为定值?若存在,求出点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽粒,古称角黍,是端午节大家都会品尝的食品.如图,平行四边形形状的纸片是由六个边长为2的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为_________;若该六面体内有一球,当该球体积最大时,球的表面积是__________.
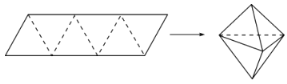
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,肥胖人数不断增多.世界卫生组织(WHO)常用身体质量指数(BMI)来衡量人体胖瘦成度以及是否健康,其计算公式是![]() .成人的BMI数值标准为:BMI
.成人的BMI数值标准为:BMI![]() 偏瘦;
偏瘦;![]() BMI
BMI![]() 为正常;
为正常;![]() BMI
BMI![]() 为偏胖;BMI
为偏胖;BMI![]() 为肥胖.某研究机构为了解某快递公司员工的身体质量指数,研究人员从公司员工体检数据中,抽取了8名员工(编号1-8)的身高
为肥胖.某研究机构为了解某快递公司员工的身体质量指数,研究人员从公司员工体检数据中,抽取了8名员工(编号1-8)的身高![]() (cm)和体重
(cm)和体重![]() (kg)数据,并计算得到他们的BMI(精确到0.1)如下表:
(kg)数据,并计算得到他们的BMI(精确到0.1)如下表:
编 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 163 | 164 | 165 | 168 | 170 | 172 | 176 | 182 |
体重(kg) | 54 | 60 | 77 | 72 | 68 | ● | 72 | 55 |
BMI(近似值) | 20.3 | 22.3 | 28.3 | 25.5 | 23.5 | 23.7 | 23.2 | 16.6 |
(1)现从这8名员工中选取3人进行复检,记抽取到BMI值为“正常”员工的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(2)研究机构分析发现公司员工的身高![]() (cm)和体重
(cm)和体重![]() (kg)之间有较强的线性相关关系,在编号为6的体检数据丢失之前调查员甲已进行相关的数据分析,并计算得出该组数据的线性回归方程为
(kg)之间有较强的线性相关关系,在编号为6的体检数据丢失之前调查员甲已进行相关的数据分析,并计算得出该组数据的线性回归方程为![]() ,且根据回归方程预估一名身高为180cm的员工体重为71kg,计算得到的其它数据如下:
,且根据回归方程预估一名身高为180cm的员工体重为71kg,计算得到的其它数据如下:![]() ,
,![]() .
.
①求![]() 的值及表格中8名员工体重的平均值
的值及表格中8名员工体重的平均值![]() .
.
②在数据处理时,调查员乙发现编号为8的员工体重数据有误,应为63kg,身高数据无误,请你根据调查员乙更正的数据重新计算线性回归方程,并据此预估一名身高为180cm的员工的体重.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: 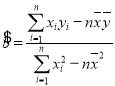 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com