练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    △ABC的三个内角A，B，C成等差数列，求证：
    c
    a+b
    +
    a
    b+c
    =1．
    考点：等差数列的性质
    专题：等差数列与等比数列
    分析：要证等式成立，只要证c2+a2-b2-ac=0 ①．根据三个内角A、B、C成等差数列求得B=
    π
    3
    ；再由余弦定理可得b2=a2+c2-ac，从而得到①成立，等式得证．
    解答： 证明：要证原式成立，只要证
    bc+c2+a2+ab
    ab+b2+ac+bc
    =1    ，
    即证bc+c2+a2+ab=ab+b2+ac+bc，即c2+a2-b2-ac=0 ①．
    而三个内角A、B、C成等差数列，由三角形内角和公式求得B=
    π
    3
    ．
    在△ABC中，由余弦定理得b2=a2+c2-2ac•cosB=a2+c2-ac，
    ∴①成立，
    故要证的等式成立．
    点评：本题主要考查余弦定理、三角形内角和公式、等差数列的性质，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    cos17°sin43°+sin163°sin47°（　　）
    A、
    1
    2
    B、-
    1
    2
    C、
    		3
    2
    D、-
    		3
    2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    把88化为五进制数是（　　）
    A、233（5）
    B、324（5）
    C、323（5）
    D、332（5）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，把边长为10的正六边形纸板剪去相同的六个角，做成一个底面为正六边形的无盖六棱柱盒子，设其高为h，体积为V（不计接缝）．
    （Ⅰ）求出体积V与高h的函数关系式并指出其定义域；
    （Ⅱ）问当h为多少时，体积V最大？最大值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知tanα=
    3
    4
    ，求值：
    （1）
    sin(2π+α)
    cos(2π-α)

    （2）
    sin(π-α)cos(π+α)cos(
    3
    2
    π+α)
    cos(3π-α)sin(3π+α)sin(
    5
    2
    π-α)
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinθ和cosθ为方程2x2-（
    		3
    +1）x+m=0的两根，求：
    （Ⅰ）
    sinθ
    1-cotθ
    +
    cosθ
    1-tanθ

    （Ⅱ）m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知复数z=（m2-8m+15）+（m2-9m+18）i在复平面内表示的点为A，实数m取什么值时：
    （1）z为实数？
    （2）z为纯虚数？
    （3）A位于第三象限？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A、B、C为锐角△ABC的三个内角，向量
    m
    =（2-2sinA，cosA+sinA）与
    n
    =（sinA-cosA，1+sinA）共线．
    （Ⅰ）求角A的大小；
    （Ⅱ）求角B的取值范围
    （Ⅲ）求函数y=2sin2B+cos
    C-3B
    2
    的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

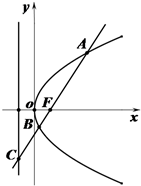    如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=6，则此抛物线的方程为
     
    ．

    查看答案和解析>>

    同步练习册答案