
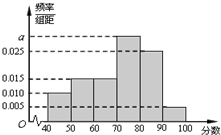
 某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.分析 (1)利用频率直方图的矩形的总面积之和为1,求分数在[70,80)内的频率为x.
(2)根据平均分、众数、中位数的求法求解即可;
(3)根据分层抽样的特点,按比例抽取即可.
解答 解:(1)设分数在[70,80)内的频率为x,根据频率分布直方图,有:
(0.01+0.015×2+0.025+0.005)×10+x=1,
可得x=0.3;
(2)估计该校高二年级学生政治成绩的平均分为:
(45×0.01+55×0.015+65×0.015+75×0.03+85×0.025+95×0.005)×10=71,
根据频率分布直方图,估计这40名学生期中政治成绩的众数为75,
因为在频率分布直方图中
第一、二、三组的频率之和为(0.010+0.015×2)×10=0.4,
所以中位数=70+$\frac{0.5-0.4}{0.3}$≈70.3;
(3)[40,50)内抽取的人数是:20×0.010×10=2人;
[50,60)内抽取的人数是:20×0.015×10=3人;
[60,70)内抽取的人数是:20×0.015×10=3人;
[70,80)内抽取的人数是:20×0.03×10=6人;
[80,90)内抽取的人数是:20×0.025×10=5人;
[9,100]取的人数是:20×0.00×10=1人,
各分数段抽取的人数分别是2人,3人,3人,6人,5人,1人.
点评 本小题主要考查频率、频数、统计和概率等知识,考查数形结合、化归与转化的数学思想方法,以及运算求解能力


科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | 12 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
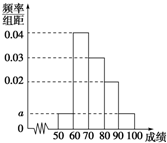 某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)A>0且ω>0,0<φ<$\frac{π}{2}$的部分图象,如图所示.
已知函数f(x)=Asin(ωx+φ)A>0且ω>0,0<φ<$\frac{π}{2}$的部分图象,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
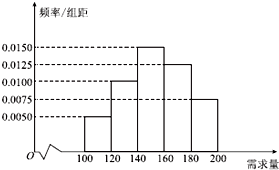 某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元;未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了160盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元;未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了160盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com