
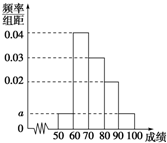
 某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
分析 (1)根据众数、平均数和中位数的定义,利用频率分布直方图即可求出结果;
(4)按表中所给的数据分别计算出数学成绩在分数段的人数,
从总人数中减去这些段内的人数即可得出数学成绩在[50,80)之外的人数.
解答 解:(1)根据频率分别直方图得,小组[60,70)高度最高,故众数是$\frac{60+70}{2}$=65;
依题意得,10(2a+0.02+0.03+0.04)=1,解得a=0.005;
这100名学生语文成绩的平均分为:
55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73(分);
设中位数为70+x分,则由0.005×10+0.04×10+0.03x=0.5,
解得x=$\frac{5}{3}$,
∴这100名学生语文成绩的中位数约为71.7(分);
(2)数学成绩在[50,60)的人数为:100×0.05=5,
数学成绩在[60,70)的人数为:100×0.4×$\frac{1}{2}$=20,
数学成绩在[70,80)的人数为:100×0.3×$\frac{4}{3}$=40,
所以数学成绩在[50,80)之外的人数为:100-5-20-40=35.
点评 本题考查了频率分布估计总体分布以及频率分布直方图的应用问题,是基础题目.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p为假 | B. | ¬q为真 | C. | p∧q为假 | D. | p∨q为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
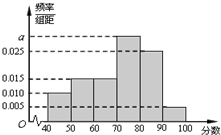 某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com