
分析 设每年新增汽车为x万辆,从2014年起该城市第n年末的汽车保有量为an,依题意可知b1=30,根据题意{an-20x}是以0.95为公比,以2-20x为首项的等比数列,判断出数列的单调性,然后利用数列的极限求得问题的答案.
解答 解:设每年新增汽车为x万辆,从2014年起该城市第n年末的汽车保有量为an
则an=(1-5%)an-1+x=0.95an-1+x(n≥2),即an-20x=0.95(an-1-20x)
∴{an-20x}是以0.95为公比,以2-20x为首项的等比数列
∴$a{\;}_n-20x=(2-20x)•{0.95^{n-1}}$,即${a_n}=20x+(2-20x)•{0.95^{n-1}}$…(7分)
(1)当2-20x≥0即x≤0.1时,an≤an-1≤…≤a1=2
(2)当2-20x<0即x>0.1时,数列{an}为递增数列,且n→+∞时,an→20x
由题20x≤5,即x≤0.25(万辆)…(11分)
综上,每年新增汽车不应超过0.25万辆.…(12分)
点评 本题主要考查了数列的应用,以及数列与不等式的综合.考查了学生综合分析问题和解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | 12 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
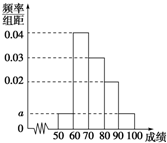 某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)A>0且ω>0,0<φ<$\frac{π}{2}$的部分图象,如图所示.
已知函数f(x)=Asin(ωx+φ)A>0且ω>0,0<φ<$\frac{π}{2}$的部分图象,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com