
���� ����������¼����ʳ˷���ʽ��⣮
��� �⣺�߳�����ָ߶���6�ࣩ��ʤ�ĸ�����$\frac{1}{2}$��
����ÿ�ֱ����߶���6�ࣩ��ʤ�ĸ��ʶ���$\frac{2}{3}$��
���ֱ�������������
��߶���6�ࣩ��3��0��ʤ�ĸ���Ϊp=��$\frac{2}{3}$��3=$\frac{8}{27}$��
�ʴ�Ϊ��$\frac{8}{27}$��
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע��������¼����ʳ˷���ʽ�ĺ������ã�


 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
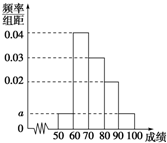 ij��100��ѧ�����п������ijɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]��
ij��100��ѧ�����п������ijɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]��| ������ | [50��60�� | [60��70�� | [70��80�� | [80��90�� |
| x��y | 1��1 | 2��1 | 3��4 | 4��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 48 | B�� | 56 | C�� | 60 | D�� | 68 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����f��x��=Asin����x+�գ�A��0�Ҧأ�0��0���գ�$\frac{��}{2}$�IJ���ͼ����ͼ��ʾ��
��֪����f��x��=Asin����x+�գ�A��0�Ҧأ�0��0���գ�$\frac{��}{2}$�IJ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\sqrt{3}$ | B�� | -1 | C�� | 0 | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com