
分析 由已知中函数f(x)=$\left\{{\begin{array}{l}{{f_1}(x),x∈[0,\frac{1}{2})}\\{{f_2}(x),x∈[\frac{1}{2},1]}\end{array}}$,其中f1(x)=-2(x-$\frac{1}{2}$)2+1;f2(x)=-2x+2,根据x0∈[0,$\frac{1}{2}$),x1=f(x0),f(x1)=x0,构造方程,解得答案.
解答 解:当x0∈[0,$\frac{1}{2}$),x1=f(x0)=-2(x0-$\frac{1}{2}$)2+1∈[$\frac{1}{2}$,1),
∴f(x1)=-2x1+2=-2[-2(x0-$\frac{1}{2}$)2+1]+2=x0,
即4x02-3x0+1=0,解得:x0=$\frac{1}{4}$,或x0=1(舍去),
故x0=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 本题考查的知识点是分段函数的应用,方程思想,难度不大,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
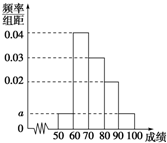 某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)A>0且ω>0,0<φ<$\frac{π}{2}$的部分图象,如图所示.
已知函数f(x)=Asin(ωx+φ)A>0且ω>0,0<φ<$\frac{π}{2}$的部分图象,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com