
| A. | p为假 | B. | ¬q为真 | C. | p∧q为假 | D. | p∨q为真 |
分析 令2x+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z,可得函数的对称轴,即可判断命题P是否正确;将含有绝对值符合的函数转化为分段函数求单调区间,来判断命题q是否正确,再利用复合命题真值表分析求解.
解答 解:∵函数$y=sin(2x+\frac{π}{6})$,令2x+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z,解得:x=kπ+$\frac{π}{6}$,k∈Z,当k=0时,x=$\frac{π}{6}$是函数$y=sin(2x+\frac{π}{6})$的对称轴,
∴命题P正确;
∵函数y=|3x-1|=$\left\{\begin{array}{l}{{3}^{x}-1}&{x≥0}\\{1-{3}^{x}}&{x<0}\end{array}\right.$,
∴函数在(0,+∞)上是增函数,在(-∞,0)上是减函数,故命题q错误.
根据复合命题真值表,A错误;B正确;C正确;D错误.
故选:A.
点评 本题借助考查命题的真假判断,考查正弦函数的对称性及指数函数的单调性,属于基础题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
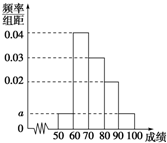 某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 56 | C. | 60 | D. | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com