Question

设实数x，y满足

2x+y-2≥0 y≥2x-2 y≤2

，则x²+y²的取值范围是（　　）

• A．[

  4

  5

  ，8]
• B．[1，2

  2

  ]
• C．[1，8]
• D．[

  2 5

  5

  ，2

  2

  ]

Answer 1

分析：由题意，画出题中不等式组表示的平面区域，得到如图的三角形及其内部，设P（x，y）是区域内的动点，由两点间的距离公式可得：z=x²+y²=|OP|²，再运动点P并加以观察即可求出z=x²+y²的取值范围．

解答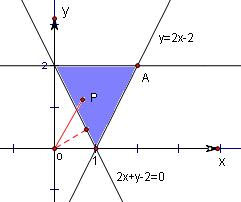：解：画出不等式组

2x+y-2≥0 y≥2x-2 y≤2

表示的平面区域如图，
得到三角形及其内部，其中A（1，1），
设P（x，y）是区域内的动点，可得z=x²+y²=|OP|²，
运动点P，当点P与A重合时，|OP|取到最大值，
此时|OP|≤|OA|=2²+2²=8，
当P与原点O在直线2x+y-2=0上的射影重合时，|OP|取到最小值，此时|OP|=

2

5

，
则x²+y²的取值范围是[

4

5

，8]．
故选A．

点评：本题给出不等式组，求目标函数z=x²+y²的取值范围．着重考查了两点的距离公式和简单线性规划等知识，属于基础题．