
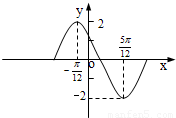
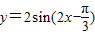
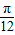 ,2)点和(-
,2)点和(-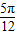 ,2),我们易分析出函数的最大值,最小值,周期,然后可以求出A,ω,φ值后,即可得到函数y=Asin(ωx+ϕ)的解析式.
,2),我们易分析出函数的最大值,最小值,周期,然后可以求出A,ω,φ值后,即可得到函数y=Asin(ωx+ϕ)的解析式.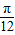 ,2)点和(-
,2)点和(-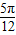 ,2)
,2)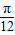 ,2)代入得
,2)代入得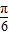 +ϕ=
+ϕ=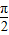 +2kπ,k∈Z,
+2kπ,k∈Z,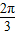 +2kπ,k∈Z,
+2kπ,k∈Z,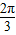
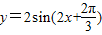
 |最大值-最小值|,|ω|=
|最大值-最小值|,|ω|= ,φ=L•ω(L是函数图象在一个周期内的第一点的向左平移量).
,φ=L•ω(L是函数图象在一个周期内的第一点的向左平移量). 

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若|
如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若|| OP |
| 10 |
| OP |
| OA |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com