
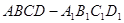 中.
中.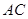 与
与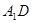 所成角的大小;
所成角的大小;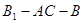 的正切值.
的正切值.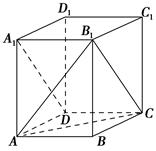
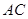 与
与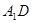 所成角为
所成角为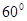 ;(Ⅱ)二面角
;(Ⅱ)二面角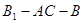 的正切值为
的正切值为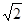 。
。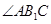 就是异面
就是异面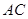 与
与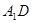 所成角,然后解三角形
所成角,然后解三角形 求此角即可.
求此角即可.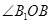 就是二面角
就是二面角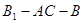 的平面角,然后再直角三角形B1BO中求此角即可.
的平面角,然后再直角三角形B1BO中求此角即可.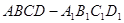 中,
中, --------------------1
--------------------1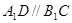 ,--------------------------- 2
,--------------------------- 2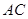 与
与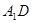 所成角………………3
所成角………………3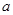
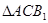 中,AC=B1A=B1C=
中,AC=B1A=B1C=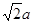 ,………………………….5
,………………………….5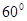
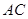 与
与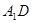 所成角为
所成角为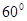 ……………………………..6
……………………………..6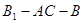 的平面角.---------------------------10
的平面角.---------------------------10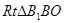 中, B1B=
中, B1B=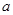 ,BO=
,BO=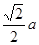 --------------------12
--------------------12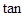 ∠B1OB=
∠B1OB=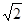
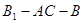 的正切值为
的正切值为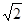 ---------------------13.
---------------------13.

科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
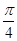 时,AE=( )
时,AE=( )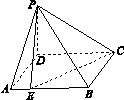
| A.1 | B. | C.2- | D.2- |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 所在的平面为
所在的平面为 ,直角坐标系
,直角坐标系 所在的平面为
所在的平面为 ,且二面角
,且二面角 的大小等于
的大小等于 .已知
.已知 内的曲线
内的曲线 的方程是
的方程是 ,则曲线
,则曲线 在
在 内的射影的曲线方程是________ .
内的射影的曲线方程是________ .
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
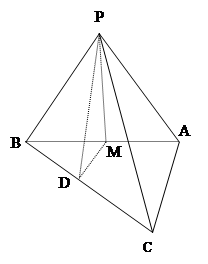
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.60° | B.90° | C.45° | D.30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com