已知
m=(cos

,sin

),
n=(cos

,sin

),且满足|
m+
n|=

。
(1)求角A的大小;
(2)若

,试判断△ABC的形状。
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
(2011•潍坊二模)已知
=(cos?x,sin?x),=(cos?x,2cos?x-sin?x),?>0,函数
f(x)=•+||,x
1,x
2是集合M={x|f(x)=1}中任意两个元素,且|x
1-x
2|的最小值为
.
(1)求?的值.
(2)在△ABC中,a,b,c分别是A,B,C的对边.
f(A)=2,c=2,S△ABC=,求a的值.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知
=(sinωx+cosωx,2sinωx),
=(cosωx-sinωx,
cosωx),(ω>0),若f(x)=
•且
f(-x)=f(x),f(x)在(0,
)内有最大值无最小值.
(1)求f(x)的最小正周期;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,f(A)=1,其面积
S△ABC=,求△ABC周长的最小值.
查看答案和解析>>
科目:高中数学
来源:
题型:
(2012•上海)定义向量
=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为
=(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S.
(1)设g(x)=3sin(x+
)+4sinx,求证:g(x)∈S;
(2)已知h(x)=cos(x+α)+2cosx,且h(x)∈S,求其“相伴向量”的模;
(3)已知M(a,b)(b≠0)为圆C:(x-2)
2+y
2=1上一点,向量
的“相伴函数”f(x)在x=x
0处取得最大值.当点M在圆C上运动时,求tan2x
0的取值范围.
查看答案和解析>>
科目:高中数学
来源:高考真题
题型:解答题
定义向量
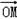
=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为

=(a,b)(其中O为坐标原点),记平面内所有向量的“相伴函数”构成的集合为S。
(1)设g(x)=3sin(x+

)+4sinx,求证:g(x)∈S;
(2)已知h(x)=cos(x+α)+2cosx,且h(x)∈S,求其“相伴向量”的模;
(3)已知M(a,b)(b≠0)为圆C:(x-2)
2+y
2=1上一点,向量

的“相伴函数”f(x)在x=x
0处取得最大值,当点M在圆C上运动时,求tan2x
0的取值范围。
查看答案和解析>>
科目:高中数学
来源:2012年上海市春季高考数学试卷(解析版)
题型:解答题
定义向量

=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为

=(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S.
(1)设g(x)=3sin(x+

)+4sinx,求证:g(x)∈S;
(2)已知h(x)=cos(x+α)+2cosx,且h(x)∈S,求其“相伴向量”的模;
(3)已知M(a,b)(b≠0)为圆C:(x-2)
2+y
2=1上一点,向量

的“相伴函数”f(x)在x=x
处取得最大值.当点M在圆C上运动时,求tan2x
的取值范围.
查看答案和解析>>

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案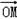 =(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为
=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为 =(a,b)(其中O为坐标原点),记平面内所有向量的“相伴函数”构成的集合为S。
=(a,b)(其中O为坐标原点),记平面内所有向量的“相伴函数”构成的集合为S。 )+4sinx,求证:g(x)∈S;
)+4sinx,求证:g(x)∈S; 的“相伴函数”f(x)在x=x0处取得最大值,当点M在圆C上运动时,求tan2x0的取值范围。
的“相伴函数”f(x)在x=x0处取得最大值,当点M在圆C上运动时,求tan2x0的取值范围。 =(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为
=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为 =(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S.
=(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S. )+4sinx,求证:g(x)∈S;
)+4sinx,求证:g(x)∈S; 的“相伴函数”f(x)在x=x处取得最大值.当点M在圆C上运动时,求tan2x的取值范围.
的“相伴函数”f(x)在x=x处取得最大值.当点M在圆C上运动时,求tan2x的取值范围.