
 :
: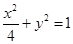 .
.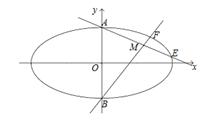
 的短轴端点分别为
的短轴端点分别为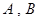 (如图),直线
(如图),直线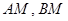 分别与椭圆
分别与椭圆 交于
交于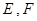 两点,其中点
两点,其中点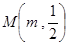 满足
满足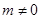 ,且
,且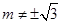 .
.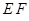 与
与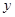 轴交点的位置与
轴交点的位置与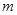 无关;
无关;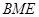 面积是∆
面积是∆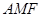 面积的5倍,求
面积的5倍,求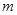 的值;
的值;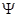 :
: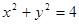 .
.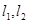 是过点
是过点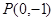 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中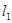 交圆
交圆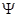 于
于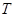 、
、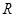 两点,
两点,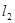 交椭圆
交椭圆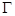 于另一点
于另一点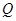 .求
.求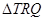 面积取最大值时直线
面积取最大值时直线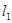 的方程.
的方程.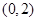 ;②
;②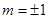 ;(2)
;(2) 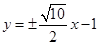 .
.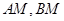 的方程,然后把直线
的方程,然后把直线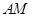 方程与椭圆方程联立,求得
方程与椭圆方程联立,求得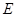 点坐标,同理求得
点坐标,同理求得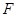 点坐标,从而得到直线
点坐标,从而得到直线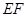 的方程,令
的方程,令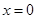 ,求出
,求出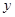
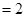 ,与
,与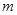 无关;②两个三角形∆
无关;②两个三角形∆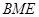 与∆
与∆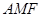 有一对对顶角
有一对对顶角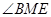 和
和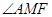 ,故面积用公式
,故面积用公式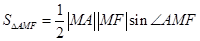 ,
,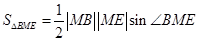 表示,那么面积比就为
表示,那么面积比就为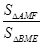
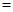
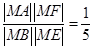 ,即
,即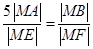 ,这个比例式可以转化为点的横坐标之间(或纵坐标)的关系式,从而求出
,这个比例式可以转化为点的横坐标之间(或纵坐标)的关系式,从而求出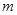 ;(2)仍采取基本方法,设
;(2)仍采取基本方法,设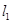 的方程为
的方程为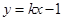 ,则
,则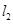 的方程为
的方程为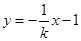 ,直线
,直线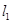 与圆
与圆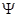 相交于
相交于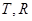 ,弦
,弦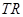 的长可用直角三角形法求,(弦心距,半径,半个弦长构成一个直角三角形),
的长可用直角三角形法求,(弦心距,半径,半个弦长构成一个直角三角形),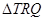 的高为
的高为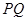 是直线
是直线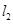 与椭圆相交的弦长,用公式
与椭圆相交的弦长,用公式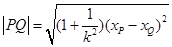 来求,再借助于基本不等式求出最大值及相应的
来求,再借助于基本不等式求出最大值及相应的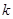 值,也即得出
值,也即得出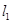 的方程.
的方程.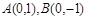 ,M (m,
,M (m,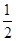 ),且
),且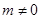 ,
,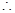 直线AM的斜率为k1=
直线AM的斜率为k1= ,直线BM斜率为k2=
,直线BM斜率为k2=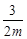 ,
, 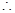 直线AM的方程为y=
直线AM的方程为y=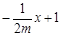 ,直线BM的方程为y=
,直线BM的方程为y=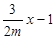 ,
,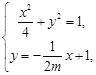 得
得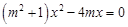 ,
,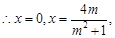
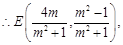
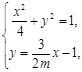 得
得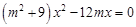 ,
,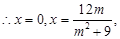
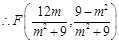 ;
;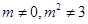 ,
,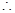 直线EF的斜率
直线EF的斜率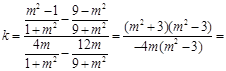
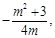
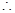 直线EF的方程为
直线EF的方程为 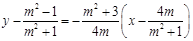 ,
,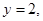
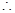 EF与y轴交点的位置与m无关.
EF与y轴交点的位置与m无关.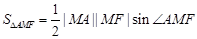 ,
,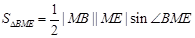 ,
,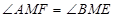 ,
,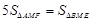 ,
,
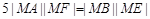 ,
,
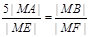 ,
,
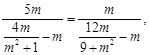
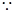
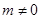 ,
,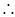 整理方程得
整理方程得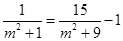 ,即
,即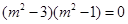 ,
,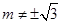 ,
,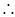
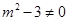 ,
,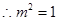 ,
,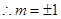 为所求.
为所求.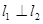 ,且都过点
,且都过点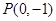 ,所以设直线
,所以设直线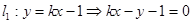 ,
,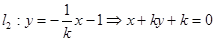 ,
,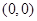 到直线
到直线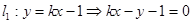 的距离为
的距离为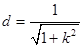 ,
,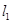 被圆
被圆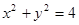 所截的弦
所截的弦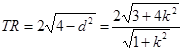 ;
;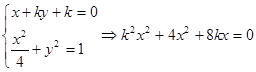 ,所以
,所以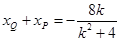 所以
所以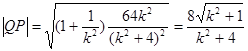
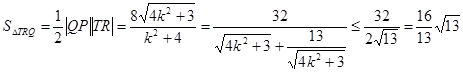
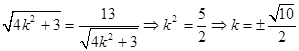 时等号成立,
时等号成立,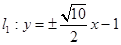


科目:高中数学 来源:不详 题型:解答题
 的离心率为
的离心率为 ,长轴长为
,长轴长为 .
. 交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足
交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足 ,若存在,求出点M的坐标;若不存在,请说明理由.
,若存在,求出点M的坐标;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的两顶点坐标
的两顶点坐标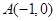 ,
,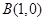 ,圆
,圆 是
是 的内切圆,在边
的内切圆,在边 ,
, ,
, 上的切点分别为
上的切点分别为 ,
, (从圆外一点到圆的两条切线段长相等),动点
(从圆外一点到圆的两条切线段长相等),动点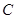 的轨迹为曲线
的轨迹为曲线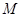 .
.
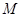 的方程;
的方程; 与曲线
与曲线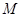 的另一交点为
的另一交点为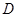 ,当点
,当点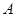 在以线段
在以线段 为直径的圆上时,求直线
为直径的圆上时,求直线 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
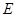 的两个焦点坐标是
的两个焦点坐标是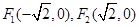 ,且离心率为
,且离心率为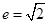 ;
;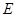 的方程;
的方程;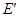 表示曲线
表示曲线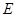 的
的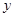 轴左边部分,若直线
轴左边部分,若直线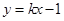 与曲线
与曲线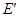 相交于
相交于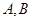 两点,求
两点,求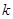 的取值范围;
的取值范围;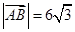 ,且曲线
,且曲线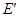 上存在点
上存在点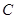 ,使
,使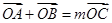 ,求
,求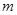 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
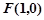 ,点
,点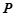 是点
是点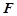 关于
关于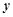 轴的对称点,过点
轴的对称点,过点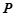 的直线交抛物线于
的直线交抛物线于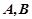 两点。
两点。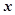 轴上是否存在不同于点
轴上是否存在不同于点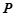 的一点
的一点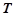 ,使得
,使得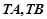 与
与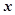 轴所在的直线所成的锐角相等,若存在,求出定点
轴所在的直线所成的锐角相等,若存在,求出定点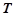 的坐标,若不存在说明理由。
的坐标,若不存在说明理由。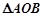 的面积为
的面积为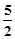 ,求向量
,求向量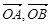 的夹角;
的夹角;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 是平面内与定点
是平面内与定点 和定直线
和定直线 的距离的积等于
的距离的积等于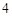 的点的轨迹.给出下列四个结论:
的点的轨迹.给出下列四个结论: 过坐标原点;
过坐标原点; 关于
关于 轴对称;
轴对称; 与
与 轴有
轴有 个交点;
个交点; 在曲线
在曲线 上,则
上,则 的最小值为
的最小值为 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com