
【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的列联表:
同意限定区域停车 | 不同意限定区域停车 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则认为“是否同意限定区域停产与家长的性别有关”的把握约为__________.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.005 | 0.001 |
| 3.841 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
【题目】某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图所示.根据学生体质健康标准,成绩不低于76的为优良. 
(1)写出这组数据的众数和中位数;
(2)将频率视为概率.根据样本估计总体的思想,在该校学生中任选3人进行体质健康测试,求至少有1人成绩是“优良”的概率;
(3)从抽取的12人中随机选取3人,记ξ表示成绩“优良”的学生人数,求ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn= ![]() ﹣
﹣ ![]() (n∈N*).
(n∈N*).
(1)求数列{an}的通项公式;
(2)若bn=anlog3an , 求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中, ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2﹣2ax+1(a为常数)
(1)讨论函数f(x)的单调性;
(2)若对任意的a∈(1, ![]() ),都存在x0∈(0,1]使得不等式f(x0)+lna>m(a﹣a2)成立,求实数m的取值范围.
),都存在x0∈(0,1]使得不等式f(x0)+lna>m(a﹣a2)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中,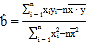 ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax,g(x)=ex﹣ax,其中a为实数.
(1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(﹣1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com