
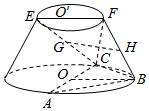
 在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.分析 (Ⅰ)取FC中点Q,连结GQ、QH,推导出平面GQH∥平面ABC,由此能证明GH∥平面ABC.
(Ⅱ)由AB=BC,知BO⊥AC,以O为原点,OA为x轴,OB为y轴,OO′为z轴,建立空间直角坐标系,利用向量法能求出二面角F-BC-A的余弦值.
解答 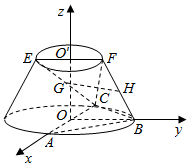 证明:(Ⅰ)取FC中点Q,连结GQ、QH,
证明:(Ⅰ)取FC中点Q,连结GQ、QH,
∵G、H为EC、FB的中点,
∴GQ$\underset{∥}{=}$$\frac{1}{2}EF$,QH$\stackrel{∥}{=}$$\frac{1}{2}BC$,
又∵EF∥BO,∴GQ∥BO,
∴平面GQH∥平面ABC,
∵GH?面GQH,∴GH∥平面ABC.
解:(Ⅱ)∵AB=BC,∴BO⊥AC,
又∵OO′⊥面ABC,
∴以O为原点,OA为x轴,OB为y轴,OO′为z轴,建立空间直角坐标系,
则A($2\sqrt{3}$,0,0),C(-2$\sqrt{3}$,0,0),B(0,2$\sqrt{3}$,0),O′(0,0,3),F(0,$\sqrt{3}$,3),
$\overrightarrow{FC}$=(-2$\sqrt{3}$,-$\sqrt{3}$,-3),$\overrightarrow{CB}$=(2$\sqrt{3}$,2$\sqrt{3}$,0),
由题意可知面ABC的法向量为$\overrightarrow{O{O}^{'}}$=(0,0,3),
设$\overrightarrow{n}$=(x0,y0,z0)为面FCB的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{FC}=0}\\{\overrightarrow{n}•\overrightarrow{CB}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-2\sqrt{3}{x}_{0}-\sqrt{3}{y}_{0}-3{z}_{0}=0}\\{2\sqrt{3}{x}_{0}+2\sqrt{3}{y}_{0}=0}\end{array}\right.$,
取x0=1,则$\overrightarrow{n}$=(1,-1,-$\frac{\sqrt{3}}{3}$),
∴cos<$\overrightarrow{O{O}^{'}}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{O{O}^{'}}•\overrightarrow{n}}{|\overrightarrow{O{O}^{'}}|•|\overrightarrow{n}|}$=-$\frac{\sqrt{7}}{7}$.
∵二面角F-BC-A的平面角是锐角,
∴二面角F-BC-A的余弦值为$\frac{\sqrt{7}}{7}$.
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长度 | ||
| C. | 向上平行移动$\frac{π}{3}$个单位长度 | D. | 向下平行移动$\frac{π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
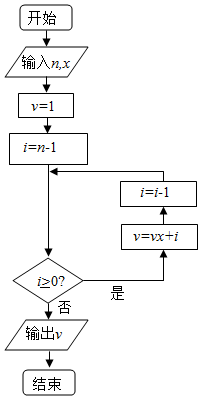 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( )| A. | 9 | B. | 18 | C. | 20 | D. | 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com