
 的解可视为函数
的解可视为函数 的图像与函数
的图像与函数 的图像交点的横坐标.若方程
的图像交点的横坐标.若方程 的各个实根
的各个实根 所对应的点
所对应的点 (
( =1,2,…,k)均在直线
=1,2,…,k)均在直线 的同侧(不包括在直线上),则实数
的同侧(不包括在直线上),则实数 的取值范围是______.
的取值范围是______.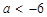 或
或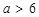
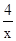
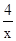 的交点的横坐标,而曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的,若交点(xi,
的交点的横坐标,而曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的,若交点(xi,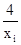 )(i=1,2,k)均在直线y=x的同侧,因直线y=x与y=
)(i=1,2,k)均在直线y=x的同侧,因直线y=x与y=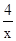 交点为:(-2,-2),(2,2);所以结合图象可得a>0, x3+a>-2,x<-2,或a<0, x3+a<2,x>2,解得a>6或a<-6.故答案为:a>6或a<-6。
交点为:(-2,-2),(2,2);所以结合图象可得a>0, x3+a>-2,x<-2,或a<0, x3+a<2,x>2,解得a>6或a<-6.故答案为:a>6或a<-6。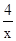 ,分别作出左右两边函数的图象:分a>0与a<0讨论,可得答案。
,分别作出左右两边函数的图象:分a>0与a<0讨论,可得答案。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com