考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)取AC的中点O,连接OF,OB,以O为原点,分别以OA,OB,OF所在直线为x轴,y轴,z轴建立空间直角坐标系,证明FB⊥AE,FB⊥AC,即可证明FB⊥平面AEC;
(2)求出平面AEF的法向量、平面AEC的一个法向量,利用向量的夹角公式,即可求二面角F-AE-C的余弦值.
解答:
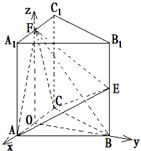
(1)证明:取AC的中点O,连接OF,OB,则有A
1A∥FO,故FO⊥平面ABC,
在正三角形ABC中,O是AC的中点,故OB⊥AC,OA=OC=1,OB=
,
如图,以O为原点,分别以OA,OB,OF所在直线为x轴,y轴,z轴建立空间直角坐标系,则O(0,0,0),A(1,0,0),B(0,
,0),C(-1,0,0),E(0,
,
),F(0,0,
),
∴
=(0,
,-
),
=(-1,
,
),
=(-2,0,0),
=(-1,0,
),
∵
•=(0,
,-
)•(-1,
,
)=0,
∴
⊥,即FB⊥AE,
又∵
•=(0,
,-
)•(-2,0,0),
∴
⊥,即FB⊥AC,
而AE∩AC=A,∴FB⊥平面ABC; …(6分)
(2)解:设平面AEF的法向量为
=(a,b,c),
则
,令c=
,则a=6,b=
,
即
=(6,
,
),由(1)知平面AEC的一个法向量为
,
设二面角F-AE-C的平面角为θ,易知
0<θ<,
∴cosθ=|
|=
. …(12分)
点评:本题考查线面垂直,考查平面与平面所成的角,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

 已知正三棱柱ABC-A1B1C1中,AB=2,AA1=
已知正三棱柱ABC-A1B1C1中,AB=2,AA1= (1)证明:取AC的中点O,连接OF,OB,则有A1A∥FO,故FO⊥平面ABC,
(1)证明:取AC的中点O,连接OF,OB,则有A1A∥FO,故FO⊥平面ABC,

 如图,△ABC中,
如图,△ABC中,