
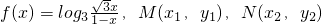 是f(x)图象点的两点,横坐标为
是f(x)图象点的两点,横坐标为 的点P是M,N的中点.
的点P是M,N的中点.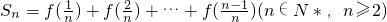 ,
,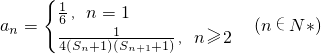 ,Tn为数列{an}前n项和,当Tn<m(Sn+1+1)对一切n∈N*都成立时,试求实数m的取值范围.
,Tn为数列{an}前n项和,当Tn<m(Sn+1+1)对一切n∈N*都成立时,试求实数m的取值范围.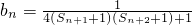 ,Bn为数列{bn}前n项和,证明:
,Bn为数列{bn}前n项和,证明: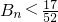 .
.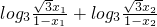 =
=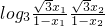
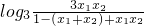 =1
=1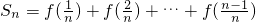 ①
①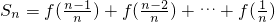 ②
② ,
,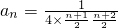 =
=
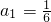 也适合上式,故
也适合上式,故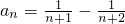
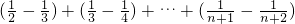 =
=
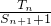 =
=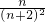 恒成立,
恒成立,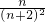 =
=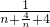
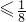 ,
, ,+∞)
,+∞)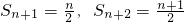 ,
,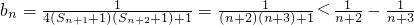
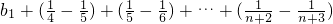
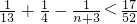
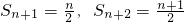 ,代入可得bn,由不等式的放缩法和裂项相消法可证.
,代入可得bn,由不等式的放缩法和裂项相消法可证.

科目:高中数学 来源: 题型:
| ||
| 1-x |
| 1 |
| 2 |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
|
| 1 |
| 4(Sn+1+1)(Sn+2+1)+1 |
| 17 |
| 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 1-x |
| 1 |
| 2 |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| 4(Sn+1+1)(Sn+2+1)+1 |
| 17 |
| 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:022
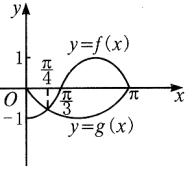
己知函数y=f(x)是偶函数,y=g(x)是奇函数,它们是定义域为[-π,π],且它们在x![]() [0,π]上的图象如图所示,则不等式
[0,π]上的图象如图所示,则不等式![]() <0的解集是 ________ 。
<0的解集是 ________ 。
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:022
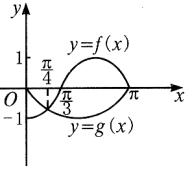
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com