解:因为当x<0时,f(x)=ax
2-x-5,其关于坐标原点对称图象的解析式为g(x)=-ax
2-x+5,所以函数f(x)的“靓点”就是g(x)=-ax
2-x+5(x>0)与t(x)=b•2
x-cx+3(x>0)这两个函数图象交点的横坐标.
(1)当a=b=c=0时,g(x)=-x+5(x>0),t(x)=3(x>0)…
由
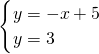
,解得x=2,所以函数f(x)的“靓点”为x=2 …
(2)当a=0且b=1时,g(x)=-x+5(x>0),t(x)=2
x-cx+3(x>0),
此时函数f(x)的“靓点”即为方程-x+5=2
x-cx+3的正根 …
方程变形为2
x=(c-1)x+2,设y
1=2
x,y
2=(c-1)x+2
因为当x=0时,y
1<y
2,结合图象知,要想f(x)在(0,1)上有且只有一个“靓点”,
则当x=1时,必须有y
1>y
2,即2>(c-1)+2,解得c<1…
(3)当c=a+1且b=0时,g(x)=-ax
2-x+5(x>0),t(x)=-(a+1)x+3(x>0),
要想f(x)恒有“靓点”,则方程-ax
2-x+5=-(a+1)x+3,
即方程ax
2-ax-2=0恒有正根 …
记h(x)=ax
2-ax-2,
①当a=0时,方程无解,不适合题意…
②当a>0时,因为h(0)=-2<0,且h(x)的图象是开口向上的抛物线,所以方程h(x)=0一定有正根,所以a>0适合题意…
③当a<0时,由
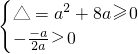
,解得a≥0或a≤-8,所以a≤-8…
综上所述,a的取值范围是a>0或a≤-8 …
(说明:其它解法,仿此给分)
分析:先根据题中新定义的“靓点”可知,当x<0时,f(x)=ax
2-x-5,其关于坐标原点对称图象的解析式为g(x)=-ax
2-x+5,所以函数f(x)的“靓点”就是g(x)=-ax
2-x+5(x>0)与t(x)=b•2
x-cx+3(x>0)这两个函数图象交点的横坐标.
(1)当a=b=c=0时,g(x)=-x+5(x>0),t(x)=3(x>0)通过解方程组
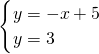
,即可得出函数f(x)的“靓点”;
(2)当a=0且b=1时,g(x)=-x+5(x>0),t(x)=2
x-cx+3(x>0),此时函数f(x)的“靓点”即为方程-x+5=2
x-cx+3的正根,通过研究此方程有正根即可求出c的取值范围;
(3)当c=a+1且b=0时,g(x)=-ax
2-x+5(x>0),t(x)=-(a+1)x+3(x>0),要想f(x)恒有“靓点”,则方程-ax
2-x+5=-(a+1)x+3,即方程ax
2-ax-2=0恒有正根.记h(x)=ax
2-ax-2,通过对字母a的讨论研究其图象与性质即可求出a的取值范围.
点评:本小题主要考查函数与方程的综合运用,考查应用所学函数数的知识、思想和方法解决实际问题的能力,建立函数式、解方程、不等式等基础知识

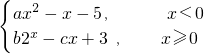 若x0>0,且点A(x0,f(x0))关于坐标原点的对称点也在f(x)的图象上,则称x0为f(x)的一个“靓点”.
若x0>0,且点A(x0,f(x0))关于坐标原点的对称点也在f(x)的图象上,则称x0为f(x)的一个“靓点”.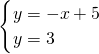 ,解得x=2,所以函数f(x)的“靓点”为x=2 …
,解得x=2,所以函数f(x)的“靓点”为x=2 …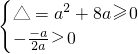 ,解得a≥0或a≤-8,所以a≤-8…
,解得a≥0或a≤-8,所以a≤-8…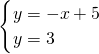 ,即可得出函数f(x)的“靓点”;
,即可得出函数f(x)的“靓点”;

 阅读快车系列答案
阅读快车系列答案