
分析 (1)利用抛物线的定义,建立方程,求出p,则抛物线方程可得,进而点A(1,m)代入,求得m的值
(2)先假设存在符合题意的直线,设出其方程,与抛物线方程联立,根据直线与抛物线方程有公共点,求得t的范围,利用直线AO与L的距离,求得t,则直线l的方程可得.
解答 解:(1)∵抛物线C:y2=2px(p>0)上一点A(1,m)到其焦点的距离为2,
∴1+$\frac{p}{2}$=2,∴p=2
∴抛物线C的方程为:y2=4x,
点A(1,m)代入,可得m=±2;
(2)由题意点A(1,-2),假设存在符合题意的直线l,其方程为y=-2x+t,
与y2=4x联立,整理得y2+2y-2t=0,
∵直线l与抛物线有公共点,
∴△=4+8t≥0,解得t≥-$\frac{1}{2}$
又∵直线OA与L的距离d=$\frac{|t|}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,求得t=±1,
∵t≥-$\frac{1}{2}$,
∴t=1,
∴符合题意的直线l存在,方程为2x+y-1=0.
点评 本题主要考查了直线,抛物线等基础知识,考查推理论证能力,运算求解能力,考查抛物线的定义,属于中档题.


科目:高中数学 来源: 题型:解答题
| 室外工作 | 室内工作 | 合计 | |
| 有呼吸系统疾病 | 150 | ||
| 无呼吸系统疾病 | 100 | ||
| 合计 | 200 |
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
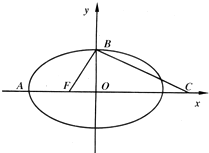 如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为$\frac{1}{2}$.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:$x+\sqrt{3}y+3=0$相切.则椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为$\frac{1}{2}$.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:$x+\sqrt{3}y+3=0$相切.则椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com