
如图,已知平行六面体ABCD—A1B1C1D1的底面为正方形,O1、O分别为上、下底面的中心,且A1在底面ABCD上的射影是O。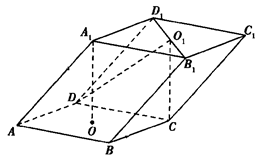
(Ⅰ)求证:平面O1DC⊥平面ABCD;
(Ⅱ)若∠A1AB=60°,求平面BAA1与平面CAA1的夹角的余弦值。
(Ⅰ)详见解析;(Ⅱ)平面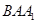 与平面
与平面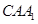 的夹角的余弦值为
的夹角的余弦值为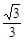 .
.
解析试题分析:(Ⅰ)求证平面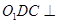 平面
平面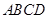 ,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,注意到
,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,注意到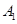 在底面
在底面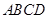 上的射影是
上的射影是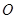 ,即
,即 平面
平面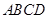 ,由图像可知只需证明
,由图像可知只需证明 即可,因此可连
即可,因此可连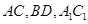 ,则
,则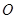 为
为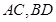 的交点,易知四边形
的交点,易知四边形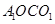 为平行四边形,从而得
为平行四边形,从而得 ,这样就得
,这样就得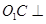 平面
平面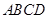 ,由面面垂直的判定定理可得结论;(Ⅱ)平面
,由面面垂直的判定定理可得结论;(Ⅱ)平面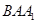 与平面
与平面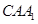 的夹角的余弦值,可用传统方法,找二面角的平面角,过点
的夹角的余弦值,可用传统方法,找二面角的平面角,过点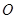 作
作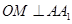 ,垂足为
,垂足为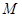 ,连接
,连接 ,由三垂线定理得
,由三垂线定理得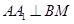 ,∴
,∴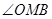 为二面角
为二面角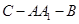 的平面角,在
的平面角,在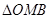 中求出此角即可;也可用空间向量法,如图分别以
中求出此角即可;也可用空间向量法,如图分别以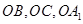 为
为 轴建立空间直角坐标系,分别找出两个半平面的法向量,利用法向量来求平面
轴建立空间直角坐标系,分别找出两个半平面的法向量,利用法向量来求平面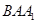 与平面
与平面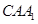 的夹角的余弦值.
的夹角的余弦值.
试题解析:(Ⅰ)连结AC,BD, A1C1,则O为AC,BD的交点O1为A1C1,B1D1的交点。
由平行六面体的性质知:A1O1∥OC且A1O1=OC,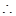 四边形A1OCO1为平行四边形, (2分)
四边形A1OCO1为平行四边形, (2分)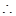 A1O∥O1C. 又∵A1O⊥平面ABCD,
A1O∥O1C. 又∵A1O⊥平面ABCD,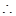 O1C⊥平面ABCD, (4分)
O1C⊥平面ABCD, (4分)
又∵O1C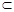 平面O1DC,
平面O1DC, 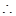 平面O1DC⊥平面ABCD。 (6分)
平面O1DC⊥平面ABCD。 (6分)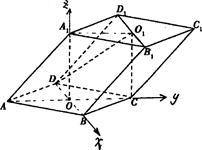
(Ⅱ)由题意可知Rt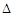 A1OB≌Rt
A1OB≌Rt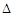 A1OA,则A1A=A1B,
A1OA,则A1A=A1B,
又∠A1AB=600,故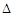 A1AB是等边三角形。 (7分)
A1AB是等边三角形。 (7分)
不妨设AB="a," 则在Rt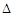 A1OA中,OA=
A1OA中,OA= a, AA1="a," OA1=
a, AA1="a," OA1= a,
a,
如图分别以OB,OC,OA1为x轴,y轴,z轴建立空间直角坐标系,
则可得坐标为A(0,- a,0), B(
a,0), B( a,0,0), A1(0,0,,
a,0,0), A1(0,0,, a) (8分)
a) (8分)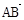 =(
=( a,
a, a,0),
a,0), 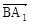 =(-
=(- a,0,
a,0, a)
a)
设平面ABA1的法向量为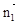 =(x,y,z)
=(x,y,z)
则由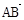 ·
·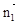 =0得x+y=0,由
=0得x+y=0,由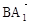 ·
·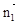 =0得x-z=0
=0得x-z=0
令x=1得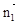 =(1,-1,1) (10分)
=(1,-1,1) (10分)
又知BD⊥平面ACC1A1,故可得平面CAA1的一个法向量为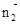 =(1,0,0)
=(1,0,0)
cosθ=|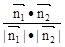 |=
|=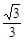
从而平


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
如图,在三棱锥S—ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°。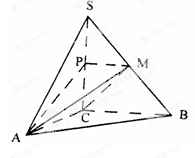
(1)求证:平面MAP⊥平面SAC。
(2)求二面角M—AC—B的平面角的正切值;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知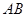 是圆的直径,
是圆的直径,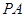 垂直圆所在的平面,
垂直圆所在的平面, 是圆上任一点,
是圆上任一点,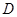 是线段
是线段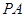 的中点,
的中点,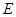 是线段
是线段 上的一点.
上的一点.
求证:(Ⅰ)若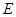 为线段
为线段 中点,则
中点,则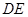 ∥平面
∥平面 ;
;
(Ⅱ)无论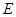 在
在 何处,都有
何处,都有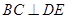 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且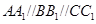 ,
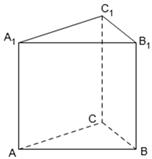
,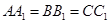 .
.
(1)求证:平面 //平面
//平面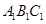 ;
;
(2)若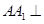 平面
平面 ,且
,且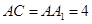 ,
,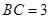 ,
,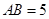 ,求证:
,求证: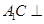 平面
平面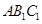 ;
;
(3)在(2)的条件下,求二面角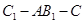 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥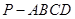 中,侧面
中,侧面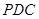 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面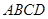 是
是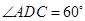 的菱形,
的菱形,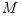 为
为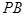 的中点.
的中点.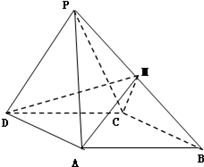
(Ⅰ)求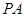 与底面
与底面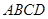 所成角的大小;
所成角的大小;
(Ⅱ)求证: 平面
平面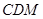 ;(Ⅲ)求二面角
;(Ⅲ)求二面角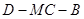 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=,PA=,∠ABC=120°,G为线段PC的中点.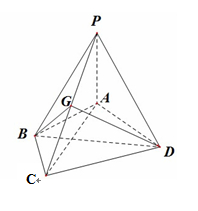
(1)证明:PA//平面BGD;
(2)求直线DG与平面PAC所成的角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com