
【题目】国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+ ![]() )+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω= .
)+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω= .
科目:高中数学 来源: 题型:
【题目】平面内到定点F(0,1)和定直线l:y=﹣1的距离之和等于4的动点的轨迹为曲线C,关于曲线C的几何性质,给出下列四个结论: ①曲线C的方程为x2=4y;
②曲线C关于y轴对称
③若点P(x,y)在曲线C上,则|y|≤2;
④若点P在曲线C上,则1≤|PF|≤4
其中,所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=log ![]() cos(
cos( ![]() ﹣2x)的递增区间是 ( )
﹣2x)的递增区间是 ( )
A.[﹣ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
B.[﹣ ![]() +kπ,kπ)(k∈Z)
+kπ,kπ)(k∈Z)
C.[ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
D.[ ![]() +kπ,
+kπ, ![]() +kπ)(k∈Z)
+kπ)(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() =1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为
=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为 ![]() .
. 
(1)求椭圆方程;
(2)若 ![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)M,N为椭圆上关于x轴对称的两点,直线PM,PN分别与x轴交于R,S,求证:|OR||OS|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)求这一天的最大温差;
(2)写出这段曲线的函数解析式.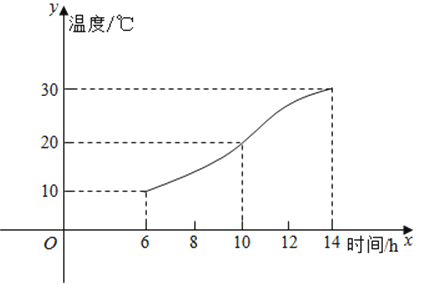
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=5,a2=2,an=2an﹣1+3an﹣2 , (n≥3) (Ⅰ)证明数列{an﹣3an﹣1}成等比数列,并求数{an}列的通项公式an;
(Ⅱ)若数列bn= ![]() (an+1+an),求数列{bn}的前n项和Sn .
(an+1+an),求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示.
(1)求函数f(x)的解析式;
(2)求g(x)=f(3x+![]() )﹣1在[﹣
)﹣1在[﹣![]() ,
, ![]() ]上的值域.
]上的值域.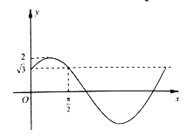
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(a+2)x+5+a,a∈R.
(Ⅰ)若方程f(x)=0有一正根和一个负根,求a的取值范围;
(Ⅱ)当x>﹣1时,不等式f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com