已知抛物线y=ax2+bx在第一象限内与直线x+y=4相切.
(Ⅰ)用b表示a,并求b的范围;
(Ⅱ)设此抛物线与x轴所围成的图形的面积为S,求S的最大值及此时a、b的值.
【答案】
分析:(I)设切点(x
,y
),根据函数在x
处的导数等于-1,以及切点在切线上又在曲线上建立方程组,可求出a与b的等式关系,最后求出b的范围即可;
(II)利用定积分表示出此抛物线与x轴所围成的图形的面积为S,然后利用定积分的运算法则求出面积S,最后利用导数研究函数的最值即可,同时求出此时的a和b.
解答:解:(I)因为直线x+y=4与抛物线y=ax
2+bx相切,设切点(x
,y
)
则f′(x
)=2ax
+b=-1,∴
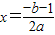
又∵
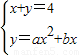
得
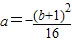
,∵0<x
,0<y
,
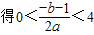
,解得b>1
(II)
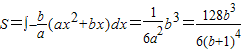
,

;
所以在b=3时,S取得极大值,也是最大值,即a=-1,b=3时,S取得最大值,且
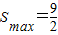
.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及用定积分求面积时,要注意明确被积函数和积分区间,属于基本知识、基本运算,属于中档题.

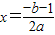
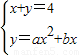 得
得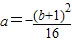 ,∵0<x,0<y,
,∵0<x,0<y,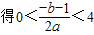 ,解得b>1
,解得b>1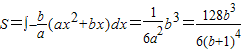 ,
, ;
;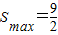 .
.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案