B
分析:由三角形的三内角成等差数列,根据等差数列的性质得到2B=A+C,再根据三角形的内角和定理可求出B的度数,进而得到sinB及cosB的值,由AB,BC及cosB的值,利用余弦定理求出AC的长,同时由sinB,AB及BC,利用三角形的面积公式求出三角形ABC的面积,最后根据底边AC及高BD,利用三角形的面积公式底乘以高的一半,列出关于BD的方程,求出方程的解即可得到高BD的长.
解答:∵A、B、C成等差数列,
∴2B=A+C,又A+B+C=π,
∴B=

,又AB=8,BC=5,
根据余弦定理得:AC
2=AB
2+BC
2-2AB•BC•cosB=64+25-40=49,
解得AC=7,
又三角形的面积S=

AB•BC•sinB=10

,
∴S=

BD•AC=10

,即BD=
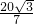
.
故选B.
点评:此题属于解三角形的题型,涉及的知识有:余弦定理,等差数列的性质,三角形的面积公式,以及特殊角的三角函数值,熟练掌握余弦定理及三角形的面积公式是解本题的关键.

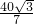
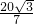
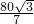

 ,又AB=8,BC=5,
,又AB=8,BC=5, AB•BC•sinB=10
AB•BC•sinB=10 ,
, BD•AC=10
BD•AC=10 ,即BD=
,即BD=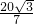 .
.
