
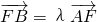 且
且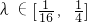 .那么k的变化范围是
.那么k的变化范围是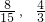 ]
]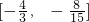
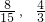 ]∪[-
]∪[- ,-
,- ]
] ]∪[
]∪[ ,+∞)
,+∞)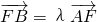 得关于x2和y2的方程组,进而求得x2=λ.得到B的坐标,根据焦点坐标可得直线的方程,进而求得直线在y轴上的截距,根据
得关于x2和y2的方程组,进而求得x2=λ.得到B的坐标,根据焦点坐标可得直线的方程,进而求得直线在y轴上的截距,根据 =
= ,判断
,判断 在
在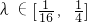 上是递减的,进而得到答案.
上是递减的,进而得到答案.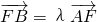 得:(x2-1,y2)=λ(1-x1,-y1),即
得:(x2-1,y2)=λ(1-x1,-y1),即  (2)
(2)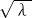 )或B(λ,-2
)或B(λ,-2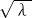 ),又F(1,0),
),又F(1,0),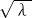 (x-1)或(λ-1)y=-2
(x-1)或(λ-1)y=-2 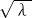 (x-1)
(x-1) 时,l在y轴上的截距为
时,l在y轴上的截距为  或-
或-
 =
= ,可知
,可知  在
在 上是递减的,
上是递减的, ≤
≤ ≤
≤ ,-
,- ≤-
≤- ≤-
≤-
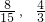 ]∪[-
]∪[- ,-
,- ]
]

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| AF |
| FB |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| FB |
| AF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| FB |
| AF |
| 1 |
| 16 |
| 1 |
| 4 |
A、[
| ||||||||
B、[-
| ||||||||
C、[
| ||||||||
D、(-∞,-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| FB |
| AF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com