
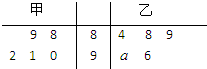
 (2013•江门一模)甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如图:
(2013•江门一模)甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如图:| 88+89+90+91+92 |
| 5 |
| 84+88+89+(90+a)+96 |
| 5 |
. |
| x甲 |
. |
| x乙 |
| 1 |
| 5 |
| 1 |
| 5 |
| 7 |
| 10 |


科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com