
 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求 的分布列和数学期望
的分布列和数学期望 .
.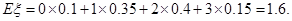
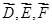 分别表示甲不胜A、乙不胜B,丙不胜C的事件.解决本小题的关键是搞清楚“红队至少两名队员获胜”包括
分别表示甲不胜A、乙不胜B,丙不胜C的事件.解决本小题的关键是搞清楚“红队至少两名队员获胜”包括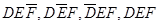 四个基本事件.
四个基本事件. 可能的取值为0,1,2,3是解决问题的第一步,然后求出每个值对应的概率,列出分布列,再根据分布列求期望.期望=每一个
可能的取值为0,1,2,3是解决问题的第一步,然后求出每个值对应的概率,列出分布列,再根据分布列求期望.期望=每一个 值与其对应的概率积之和.
值与其对应的概率积之和.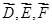 分别表示甲不胜A、乙不胜B,丙不胜C的事件.
分别表示甲不胜A、乙不胜B,丙不胜C的事件.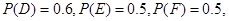
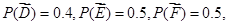
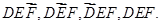
 ……6分
……6分 可能的取值为0,1,2,3.
可能的取值为0,1,2,3.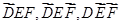 是两两互斥事件,
是两两互斥事件,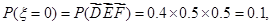
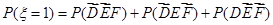
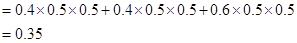
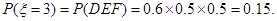
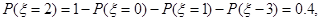 ……………………9分
……………………9分 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 |
| P | 0.1 | 0.35 | 0.4 | 0.15 |
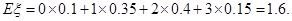 ……………………10分
……………………10分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 和
和 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中: 的分布列与期望.
的分布列与期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 13 | 13 | 5 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 8 | 12 | 5 | 3 | 1 |
| ξ | 1 | 2 | 3 |
 |  |  |  |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是一个随机变量,求随机变量
是一个随机变量,求随机变量 的分布列及数学期望
的分布列及数学期望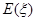 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个男生和
个男生和 个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有 种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有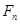 种选法.
种选法. 和
和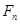 ;
;  和
和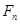 的大小(
的大小(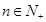 ),并用数学归纳法证明.
),并用数学归纳法证明.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 视觉 视觉 | 视觉记忆能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 | 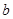 | |
| 偏高 | 2 |  | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
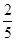 .
. 、
、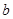 的值;
的值; ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
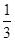 ,某
,某 表示四次实验结束时实验成功的次数与失败的次数之差的绝对
表示四次实验结束时实验成功的次数与失败的次数之差的绝对 的分布列及
的分布列及 的数学期望
的数学期望 ;
; 的解集是实数集
的解集是实数集 ”为事件
”为事件 ,求事件
,求事件 发生的概率
发生的概率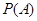 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com