练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某校为了解高一年级学生身高情况，按10％的比例对全校700名高一学生按性别进行抽样检查，测得身高频数分布表如下：
    表1：男生身高频数分布表
    身高（cm）
    		[160,165）
    		[165,170）
    		[170,175）
    		[175,180）
    		[180,185）
    		[185,190）
    频数
    		2
    		5
    		13
    		13
    		5
    		2
    表2：女生身高频数分布表
    身高（cm）
    		[150,155）
    		[155,160）
    		[160,165）
    		[165,170）
    		[170,175）
    		[175,180）
    频数
    		1
    		8
    		12
    		5
    		3
    		1
    （Ⅰ）求该校高一男生的人数；
    （Ⅱ）估计该校高一学生身高（单位：cm）在[165，180）的概率；
    （Ⅲ）在男生样本中，从身高（单位：cm）在[180，190）的男生中任选3人，设ξ表示所选3人中身高（单位：cm）在[180，185）的人数，求ξ的分布列和数学期望.
    ξ
    		1
    		2
    		3




    （I）高一男生为400人　（Ⅱ）
    ξ的分布列为:
    　　……12分
    （Ⅰ）根据分层抽样的定义即可算出所求人数；（Ⅱ）利用表格线求出频率，然后再利用频率估计概率；（Ⅲ）先求出随机变量的取值，然后求出对应的概率，进一步利用分布列和期望的定义求解
    （I）样本人数男生为40人，由分层抽样比例为10%可知全校高一男生为400人　
    （Ⅱ）由表1、2知,样本中身高在165-180 cm之间的频率,由此估计该校高一学生身高在[165，180）的概率……4分
    (Ⅲ).由题意知: ,，
    ξ
    		1
    		2
    		3




    ，……10分　　
    ξ的分布列为:
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）在第9届校园文化艺术节棋类比赛项目报名过程中，我校高二(2)班共有16名男生和14名女生预报名参加，调查发现，男、女选手中分别有10人和6人会围棋.
    （I）根据以上数据完成以下22列联表：
     
    		会围棋
    		不会围棋
    		总计
    男
    		 
    		 
    		 
    女
    		 
    		 
    		 
    总计
    		 
    		 
    		30
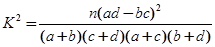    并回答能否在犯错的概率不超过0．10的前提下认为性别与会围棋有关？
    参考公式：其中n=a+b+c+d
    参考数据：

    		0.40
    		0.25
    		0.10
    		0.010

    		0.708
    		1.323
    		2.706
    		6.635
    （Ⅱ）若从会围棋的选手中随机抽取3人成立该班围棋代表队，则该代表队中既有男又
    有女的概率是多少？
    （Ⅲ）若从14名女棋手中随机抽取2人参加棋类比赛，记会围棋的人数为，求的期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本小题满分12分)
    某地区对12岁儿童瞬时记忆能力进行调查．瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人，下表为该班学生瞬时记忆能力的调查结果．例如表中听觉记忆能力为中等，且视觉记忆能力偏高的学生为3人．
        视觉        
    		视觉记忆能力
    偏低
    		中等
    		偏高
    		超常
    听觉
    记忆
    能力
    		偏低
    		0
    		7
    		5
    		1
    中等
    		1
    		8
    		3

    偏高
    		2

    		0
    		1
    超常
    		0
    		2
    		1
    		1
    由于部分数据丢失，只知道从这40位学生中随机抽取一个，视觉记忆能力恰为中等，且听觉记忆能力为中等或中等以上的概率为．
    （I）试确定、的值；
    （II）从40人中任意抽取3人，求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率；
    （III）从40人中任意抽取3人，设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为，求随机变量的数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    甲、乙两名工人加工同一种零件，两人每天加工的零件数相等，所出次品数分别为，，且和的分布列为：

    		0
    		1
    		2




     
    试比较两名工人谁的技术水平更高．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    如果甲乙两个乒乓球选手进行比赛，而且他们在每一局中获胜的概率都是，规定使用“七局四胜制”，即先赢四局者胜．
    (1)试分别求甲打完4局、5局才获胜的概率；
    (2)设比赛局数为ξ，求ξ的分布列及期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题满分10分）
    （理）红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛，甲对A，乙对B，丙对C各一盘，已知甲胜A，乙胜B，丙胜C的概率分别为0.6,0.5,0.5，假设各盘比赛结果相互独立.（Ⅰ）求红队至少两名队员获胜的概率；
    （Ⅱ）用表示红队队员获胜的总盘数，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题满分14分）张先生家住H小区，他在C科技园区工作，从家开车到公司上班有L1，L2两条路线（如图），L1路线上有A1，A2，A3三个路口，各路口遇到红灯的概率均为；L2路线上有B1，B2两个路口，各路口遇到红灯的概率依次为，．

    （1）若走L1路线，求最多遇到1次红灯的概率；
    （2）若走L2路线，求遇到红灯次数的数学期望；
    （3）按照“平均遇到红灯次数最少”的要求，请你帮助张先生从上述两条路线中选择一条最好的上班路线，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    学校文娱队的每位队员唱歌、跳舞至少会一项，已知会唱歌的有2人，会跳舞的有5人，现从中选2人．设为选出的人中既会唱歌又会跳舞的人数，且．
    （1）求文娱队的队员人数；
    （2）写出的概率分布列并计算

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    甲、乙两人独立地从六门选修课程中任选三门进行学习，记两人所选课程相同的门数为，则为     (    )
    A．1B．C．2D．

    查看答案和解析>>

    同步练习册答案