
(本题12分)某公司是专门生产健身产品的企业,第一批产品 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品 上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品
上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
(1)写出市场的日销售量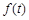 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;
(2)第一批产品A上市后的第几天,这家公司日销售利润最大,最大利润是多少?
(1)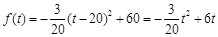
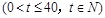 ;
;
(2)第一批产品A上市后的第27天这家公司日销售利润最大,最大利润是 万元.
万元.
解析试题分析:(1)先根据题意设f(t)=a(t-20)2+60,由f(0)=0求得a值即得日销售量f(t)(2)与第一批产品A上市时间t的关系式;
(2)先写出销售利润为g(t)万元,分类讨论:当30≤t≤40时,当0<t≤30时,分别研究它们的单调性,而t∈N,故比较g(26),g(27)即可,经计算,g(26)<g(27),故第一批产品A上市后的第27天这家公司日销售利润最大。
解:(1) 设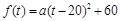 ,由
,由 可知
可知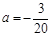
即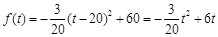
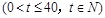 ;……………4分
;……………4分
(2) 设销售利润为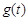 万元,则
万元,则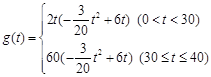 ……………………8分
……………………8分
当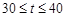 时,
时,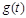 单调递减;
单调递减;
当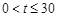 时,
时,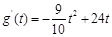 ,易知
,易知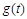 在
在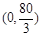 单增,
单增,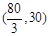 单减,而
单减,而 ,故比较
,故比较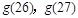 ,经计算,
,经计算,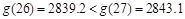 ,故第一批产品A上市后的第27天这家公司日销售利润最大,最大利润是
,故第一批产品A上市后的第27天这家公司日销售利润最大,最大利润是 万元.………………12分
万元.………………12分
考点:本试题主要考查了分段函数,以及函数与方程的思想,属于基础题.
点评:解决该试题的函数模型为分段函数,求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.


科目:高中数学 来源: 题型:解答题
(本小题共12分)已知f(x)=m(x-2m)(x+m+3),g(x)=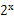 -2,若同时满足条件:
-2,若同时满足条件:
①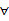 x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;②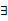 x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=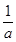 -
-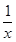 (a>0,x>0).
(a>0,x>0).
(1)用函数的单调性定义证明:f(x)在(0,+∞)上是增函数;
(2)若f(x)在[ ,2]上的值域是[
,2]上的值域是[ ,2],求实数a的值.
,2],求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com