Question

设△ABC三个内角A、B、C所对的边分别为a，b，c. 已知C＝，acosA=bcosB．

（1）求角A的大小；

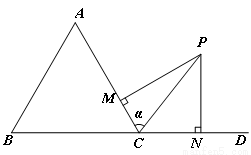
（2）如图，在△ABC的外角∠ACD内取一点P，使得PC＝2．过点P分别作直线CA、CD的垂线PM、PN，垂足分别是M、N．设∠PCA＝α，求PM＋PN的最大值及此时α的取值．

 

 

Answer 1

（1）A＝,（2）2．

【解析】

试题分析：（1）解三角形问题，一般利用正余弦定理进行变角转化. 由acosA＝bcosB及正弦定理可得sinAcosA＝sinBcosB，即sin2A＝sin2B，又A∈(0，π)，B∈(0，π)，所以有A＝B或A＋B＝．又因为C＝，得A＋B＝，与A＋B＝矛盾，所以A＝B，因此A＝．（2）求PM＋PN的最大值,需先将PM＋PN表示为α的函数解析式. 在Rt△PMC中，PM＝PC·sin∠PCM＝2sinα；在Rt△PNC中，PN＝PC·sin∠PCN＝ PC·sin(π－∠PCB) ＝2sin[π－(α＋)]＝2sin (α＋)，α∈(0，)，所以，PM＋PN＝2sinα＋2sin (α＋)＝3sinα＋cosα＝2sin(α＋).因为α∈(0，)，所以α＋∈(，)，从而有sin(α＋)∈(，1]，即2sin(α＋)∈(，2]．于是，当α＋＝，即α＝时，PM＋PN取得最大值2．

解（1）由acosA＝bcosB及正弦定理可得sinAcosA＝sinBcosB，

即sin2A＝sin2B，又A∈(0，π)，B∈(0，π)，

所以有A＝B或A＋B＝． 3分

又因为C＝，得A＋B＝，与A＋B＝矛盾，

所以A＝B，因此A＝． 6分

（2）由题设，得

在Rt△PMC中，PM＝PC·sin∠PCM＝2sinα；

在Rt△PNC中，PN＝PC·sin∠PCN＝ PC·sin(π－∠PCB)

＝2sin[π－(α＋)]＝2sin (α＋)，α∈(0，). 8分

所以，PM＋PN＝2sinα＋2sin (α＋)＝3sinα＋cosα＝2sin(α＋). 12分

因为α∈(0，)，所以α＋∈(，)，从而有sin(α＋)∈(，1]，

即2sin(α＋)∈(，2]．

于是，当α＋＝，即α＝时，PM＋PN取得最大值2． 16分

考点：正弦定理，三角函数最值