已知集合A={x|x2-7x+6≤0,x∈N*},集合B={x||x-3|≤3.x∈N*},集合M={(x,y)|x∈A,y∈B}
(1)求从集合M中任取一个元素是(3,5)的概率;
(2)从集合M中任取一个元素,求x+y≥10的概率;
(3)设ξ为随机变量,ξ=x+y,写出ξ的分布列,并求Eξ.
【答案】
分析:(1)由题意知本题是一个古典概型,试验发生包含的事件是集合M={(x,y)|x∈A,y∈B},整理A和B两个集合,得到基本事件的个数,满足条件的事件只有一个,得到结果
(2)由题意知本题是一个古典概型,试验发生包含的事件是集合M中任取一个元素共有36 种结果,满足条件的事件是x+y≥10,可以列举出来,根据古典概型概率公式得到结果.
(3)ξ可能取的值为2,3,4,5,6,7,8,9,10,11,12,分别求出相应的概率,作出ξ的分布列,然后利用离散型随机变量的期望公式求解.
解答:解:(1)设从M中任取一个元素是(3,5)的事件为B,则P(B)=
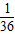
所以从M中任取一个元素是(3,5)的概率为
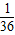
(2)设从M中任取一个元素,x+y≥10的事件为C,有
(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)
则P(C)=

,所以从M中任取一个元素x+y≥10的概率为

(3)ξ可能取的值为2,3,4,5,6,7,8,9,10,11,12
ξ的分布列为
Eξ=2×

+
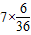
+8×
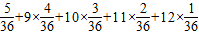
=7
点评:本题是一个通过列举来解决的概率问题,是一个实际问题,这种题目经常见到,同学们一定比较感兴趣,从这个题目上体会列举法的优越性和局限性.

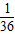
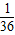
 ,所以从M中任取一个元素x+y≥10的概率为
,所以从M中任取一个元素x+y≥10的概率为
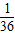

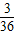
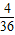
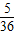
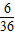
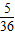
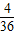
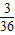
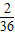
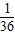
 +
+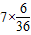 +8×
+8×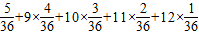 =7
=7
