
分析 先根据定积分的计算得到cosφ-sinφ=$\frac{\sqrt{7}}{4}$,再平方利用二倍角公式即可求出答案.
解答 解:$\int_0^{\frac{π}{2}}$sin(x-φ)dx=-cos(x-φ)|${\;}_{0}^{\frac{π}{2}}$=-[cos($\frac{π}{2}$-φ)-cosφ]=cosφ-sinφ=$\frac{\sqrt{7}}{4}$,
∴cos2φ+sin2φ-2cosφsinφ=$\frac{7}{16}$,
∴sin2φ=$\frac{9}{16}$
故答案为:$\frac{9}{16}$.
点评 本题考查了定积分的计算和三角函数的化简,属于基础题.


科目:高中数学 来源: 题型:选择题
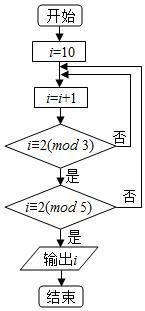 把“正整数N除以正整数m后的余数为n”记为N≡n(modm),例如8≡2(mod3).执行如图的该程序框图后,输出的i值为( )
把“正整数N除以正整数m后的余数为n”记为N≡n(modm),例如8≡2(mod3).执行如图的该程序框图后,输出的i值为( )| A. | 14 | B. | 17 | C. | 22 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1或3 | B. | 1或-3 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 |
| 1 40 2 44 3 40 4 41 5 33 6 40 7 45 8 42 9 43 | 10 36 11 31 12 38 13 39 14 43 15 45 16 39 17 38 18 36 | 19 27 20 43 21 41 22 37 23 34 24 42 25 37 26 44 27 42 | 28 34 29 39 30 43 31 38 32 42 33 53 34 37 35 49 36 39 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com