
【题目】选修4-1:几何证明选讲
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC

(1)求证:P=EDF;
(2)求证:CE·EB=EF·EP.
【答案】证明见解析.
【解析】(1)要证明两角P,EDF相等,注意到![]() ,
,![]() ,因此只要证C,EDF相等,这两个角正好是可证相似的两个三角形的对应角,这个相似由已知DE2=EF·EC可证;(2)要证明线段乘积相等,在已知圆中由相交弦定理有CE·EB=ED·EA,再看ED·EA与EF·EP的相等可由相似三角形得到.
,因此只要证C,EDF相等,这两个角正好是可证相似的两个三角形的对应角,这个相似由已知DE2=EF·EC可证;(2)要证明线段乘积相等,在已知圆中由相交弦定理有CE·EB=ED·EA,再看ED·EA与EF·EP的相等可由相似三角形得到.
试题分析:
试题解析:证明(1)∵DE2=EF·EC,
∴DE CE=EF ED.
∵DEF是公共角,
∴ΔDEF∽ΔCED. ∴EDF=C.
∵CD∥AP, ∴C= P.
∴P=EDF.----5分
(2)∵P=EDF, DEF=PEA,
∴ΔDEF∽ΔPEA.∴DE PE=EF EA.即EF·EP=DE·EA.
∵弦AD、BC相交于点E,∴DE·EA=CE·EB.∴CE·EB=EF·EP. 10分


科目:高中数学 来源: 题型:
【题目】已知在三棱锥![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() 都是正三角形,
都是正三角形,![]() .
.
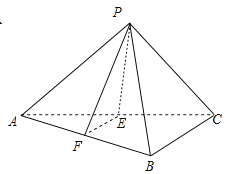
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)若点![]() 在一个表面积为
在一个表面积为![]() 的球面上,求
的球面上,求![]() 的边长.
的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下命題:
①命题 “在![]() 中,若
中,若![]() ,则
,则![]() ” 的逆命題为真命题;
” 的逆命題为真命题;
②若动点![]() 到两定点
到两定点![]() 的距离之和为
的距离之和为![]() ,则动点
,则动点![]() 的轨迹为线段
的轨迹为线段![]() ;
;
③若![]() 为假命题,则
为假命题,则![]() 都是假命題;
都是假命題;
④设![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
⑤若实数![]() 成等比数列,则圆锥曲线
成等比数列,则圆锥曲线![]() 的离心率为
的离心率为![]() ;
;
其中所有正确命题的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象与函数h(x)=x+![]() +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)若g(x)=x2·[f(x)-a],且g(x)在区间[1,2]上为增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的从高气温,下面的折线代表可能出现的最低气温.

(Ⅰ)指出最高气温与最低气温的相关性;
(Ⅱ)估计在10:00时最高气温和最低气温的差;
(Ⅲ)比较最低气温与最高气温方差的大小(结论不要求证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(3)若(2)中函数![]() 有两个极值点
有两个极值点![]()
![]() ,且不等式
,且不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,
直线![]() 与椭圆
与椭圆![]() 的一个交点为
的一个交点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的任意—点,延长
上的任意—点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的内切圆的最大周长.
的内切圆的最大周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如下:


(1)求李老师这8天“健步走”步数的平均数;
(2)从步数为16千步,17千步,18千步的6天中任选2天,设李老师这2天通过“健步走”消耗的能量和为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com