
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
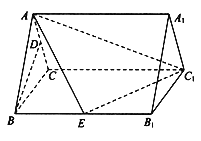
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若这个三棱柱的底面是边长为2的等边三角形,側面都是正方形,求五面体![]() 的体积.
的体积.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)由条件证明![]() 为平行四边形,故得
为平行四边形,故得![]() ,然后再由线面平行的判定定理可得结论成立.(Ⅱ)方法一:取
,然后再由线面平行的判定定理可得结论成立.(Ⅱ)方法一:取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,然后证明
,然后证明![]() 为四棱锥
为四棱锥![]() 的高,于是可得所求体积.方法二:取
的高,于是可得所求体积.方法二:取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据条件可证得
,根据条件可证得![]() 是四棱锥
是四棱锥![]() 的高,且
的高,且![]() ,然后根据
,然后根据![]() 求解.
求解.
(Ⅰ)证明:设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .
.
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]() 且
且![]() .
.
∵![]() 为
为![]() 的中点,
的中点,
∴![]() 且
且![]() .
.
∴![]() 且
且![]() ,
,
∴![]() 为平行四边形,
为平行四边形,
∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
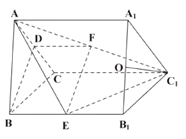
(Ⅱ)解法一:取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵侧面是正方形,
∴![]() ,
,![]() .
.
又![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() 为四棱锥
为四棱锥![]() 的高.
的高.
故所求体积![]()
![]() .
.
(Ⅱ)解法二:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵侧面都是正方形,
∴![]() ,
,![]() .
.
∵![]() 平面
平面![]() 且
且![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() .
.
∴![]() 是四棱锥
是四棱锥![]() 的高,且
的高,且![]() .
.
故所求体积![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是实系数一元二次方程
是实系数一元二次方程![]() 的虚根,记它在直角坐标平面上的对应点位
的虚根,记它在直角坐标平面上的对应点位![]() .
.
(1)若![]() 在直线
在直线![]() 上,求证:
上,求证:![]() 在圆
在圆![]() :
:![]() 上;
上;
(2)给定圆![]() ,则存在唯一的线段
,则存在唯一的线段![]() 满足:
满足:
①若![]() 在圆
在圆![]() 上,则
上,则![]() 在线段
在线段![]() 上;
上;
②若![]() 是线段
是线段![]() 上一点(非端点),则
上一点(非端点),则![]() 在圆
在圆![]() 上,写出线段
上,写出线段![]() 的表达式,并说明理由;
的表达式,并说明理由;
(3)由(2)知线段![]() 与圆
与圆![]() 之间确定了一种对应关系,通过这种对应关系的研究,填写表一(表中
之间确定了一种对应关系,通过这种对应关系的研究,填写表一(表中![]() 是(1)中圆
是(1)中圆![]() 的对应线段).
的对应线段).
表一:
线段 |
|
| |
| |
线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:
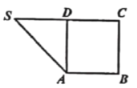
【题目】如图,在直角梯形SABC中,![]() ,D为边SC上的点,且
,D为边SC上的点,且![]() ,现将
,现将![]() 沿AD折起到达
沿AD折起到达![]() 的位置(折起后点S记为P),并使得
的位置(折起后点S记为P),并使得![]() .
.
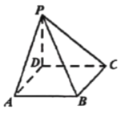
(1)求证:![]() 平面ABCD;
平面ABCD;
(2)设![]() ,
,
①若点E在线段BP上,且满足![]() ,求平面EAC与平面PDC所成的锐二面角的余弦值
,求平面EAC与平面PDC所成的锐二面角的余弦值
②设G是AD的中点,则在![]() 内(含边界)是否存在点F,使得
内(含边界)是否存在点F,使得![]() 平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,如果![]() 与
与![]() 都是整数,就称点
都是整数,就称点![]() 为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
①存在这样的直线,既不与坐标轴平行又不经过任何整点
②如果![]() 与
与![]() 都是无理数,则直线
都是无理数,则直线![]() 不经过任何整点
不经过任何整点
③直线![]() 经过无穷多个整点,当且仅当
经过无穷多个整点,当且仅当![]() 经过两个不同的整点
经过两个不同的整点
④直线![]() 经过无穷多个整点的充分必要条件是:
经过无穷多个整点的充分必要条件是:![]() 与
与![]() 都是有理数
都是有理数
⑤存在恰经过一个整点的直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,己知点
中,己知点![]() ,
,![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,满足
上的动点,满足![]() .
.
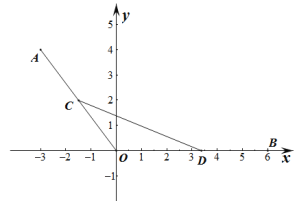
(1)若![]() 点恰好与
点恰好与![]() 点重合,求半径为
点重合,求半径为![]() 且与直线
且与直线![]() 相切于
相切于![]() 点的圆的方程;
点的圆的方程;
(2)设![]() ,求证:
,求证:![]() 的外接圆恒过定点(异于原点).
的外接圆恒过定点(异于原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南某地区![]() 年10年间梅雨季节的降雨量
年10年间梅雨季节的降雨量![]() 单位:
单位:![]() 的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
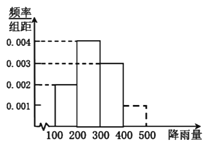
![]() 假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
![]() 老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元
老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元![]() 而乙品种杨梅的亩产量
而乙品种杨梅的亩产量![]() 亩
亩![]() 与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为
与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为![]() 元
元![]() ,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润
,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润![]() 万元
万元![]() 的期望更大?并说明理由.
的期望更大?并说明理由.
降雨量 |
|
|
|
|
亩产量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局统计了我国近10年(2009年2018年)的GDP(GDP是国民经济核算的核心指标,也是衡量一个国家或地区总体经济状况的重要指标)增速的情况,并绘制了下面的折线统计图.

根据该折线统计图,下面说法错误的是
A. 这10年中有3年的GDP增速在9.00%以上
B. 从2010年开始GDP的增速逐年下滑
C. 这10年GDP仍保持6.5%以上的中高速增长
D. 2013年—2018年GDP的增速相对于2009年—2012年,波动性较小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com