

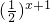
 在(0,+∞)上是减函数,可判断B,利用,y=
在(0,+∞)上是减函数,可判断B,利用,y= 是减函数,可判断C的正误;由f(x)=log2x的单调性可判断D的正误.
是减函数,可判断C的正误;由f(x)=log2x的单调性可判断D的正误. 在(0,+∞)上是减函数,故B中函数不合要求B;
在(0,+∞)上是减函数,故B中函数不合要求B; 的底数0<
的底数0< <1,y=
<1,y= 是减函数,
是减函数,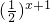 为(0,+∞)上的减函数,故C中函数不合要求;
为(0,+∞)上的减函数,故C中函数不合要求;

 智能训练练测考系列答案
智能训练练测考系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com