
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数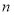 及天数如下表:
及天数如下表:
售出个数 | 10 | 11 | 12 | 13 | 14 | 15 |
天数 | 3 | 3 | 3 | 6 | 9 | 6 |
试依据以频率估计概率的统计思想,解答下列问题:
(1)计算小王某天售出该现烤面包超过13个的概率;
(2)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量.试求小王增加订购量的概率.
(3)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
(1)0.5;(2)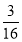 ;(3)分布列为
;(3)分布列为
利润 | 80 | 95 | 110 | 125 | 140 |
概率 | 0.1 | 0.1 | 0.1 | 0.2 | 0.5 |
数学期望为123.5元.
【解析】
试题分析:(1)由于小王某天售出该现烤面包超过13个的情况有三种:恰14个和恰15个,由题中表格易得:小王某天售出该现烤面包恰14个和恰15个的概率分别为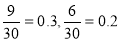 ,再由小王某天售出该现烤面包恰14个和恰15个这两个事件是互斥的,所以小王某天售出该现烤面包超过13个的概率就等于上述两个概率之和为:0.3+0.2=0.5.
,再由小王某天售出该现烤面包恰14个和恰15个这两个事件是互斥的,所以小王某天售出该现烤面包超过13个的概率就等于上述两个概率之和为:0.3+0.2=0.5.
(2)设在最近的5天中售出超过13个的天数为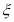 ,由于每天售出的个数要么超过13个,要么不超过13个只有这两种结果,且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变各为0.5,所以
,由于每天售出的个数要么超过13个,要么不超过13个只有这两种结果,且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变各为0.5,所以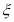 服从参数为5和0.5的二项分布,即
服从参数为5和0.5的二项分布,即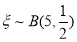 ,从而事件“小王增加订购量”的概率,即是
,从而事件“小王增加订购量”的概率,即是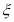 >3的概率,而
>3的概率,而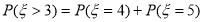 ,再由二项分布的概率公式
,再由二项分布的概率公式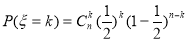 可算得事件“小王增加订购量”的概率;
可算得事件“小王增加订购量”的概率;
(3)由于小王每天订购14个现烤面包,则可设其一天的利润为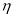 元,由已知求出
元,由已知求出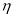 的所有可能取值,并结合题只所给条件可得到
的所有可能取值,并结合题只所给条件可得到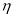 的每一个可能取值的概率,从而求得其分布列,在由数学期望公式:
的每一个可能取值的概率,从而求得其分布列,在由数学期望公式: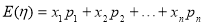 就可求得所获利润的数学期望.
就可求得所获利润的数学期望.
试题解析:(1)记事件A=“小王某天售出超过13个现烤面包”, 1分
用频率估计概率可知:
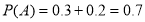 . 2分
. 2分
所以小王某天售出超过13个现烤面包的概率为0.5. 3分
(2)设在最近的5天中售出超过13个的天数为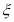 ,
,
则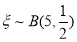 . ..5分
. ..5分
记事件B=“小王增加订购量”,
则有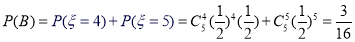 ,
,
所以小王增加订购量的概率为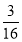 . 8分
. 8分
(3)若小王每天订购14个现烤面包,设其一天的利润为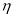 元,则
元,则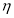 的所有可能取值为80,95,110,125,140. 9分
的所有可能取值为80,95,110,125,140. 9分
其分布列为
利润 | 80 | 95 | 110 | 125 | 140 |
概率 | 0.1 | 0.1 | 0.1 | 0.2 | 0.5 |
11分
则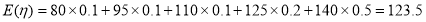
所以小王每天出售该现烤面包所获利润的数学期望为123.5元. ..13分
考点:1.概率和公式;2.二项分布;3.分布列与数学期望.


科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
命题 : “方程
: “方程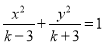 表示双曲线” (
表示双曲线” (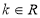 );命题
);命题 :
: 定义域为
定义域为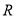 ,若命题
,若命题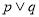 为真命题,
为真命题,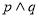 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:选择题
从1,2,3,4这4个数中,不放回地任意取两个数,两个数都是奇数的概率是( ).
A. B.
B. C.
C.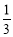 D.
D.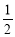
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末文科数学试卷(解析版) 题型:选择题
以下有关命题的说法错误的是( )
A.命题“若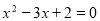 ,则
,则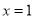 ”的逆否命题为“若
”的逆否命题为“若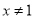 ,则
,则 ”
”
B.对于命题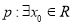 ,使得
,使得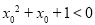 ,则
,则 ,则
,则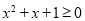
C.“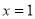 ”是“
”是“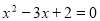 ”的充分不必要条件
”的充分不必要条件
D.若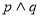 为假命题,则
为假命题,则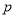 、
、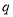 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高二下学期期末理科数学试卷(解析版) 题型:解答题
曲线C的极坐标方程为 ,以极点O为原点,极轴Ox为x的非负半轴,保持单位长度不变建立直角坐标系xoy.
,以极点O为原点,极轴Ox为x的非负半轴,保持单位长度不变建立直角坐标系xoy.
(1)求曲线C的直角坐标方程;
(2)直线l的参数方程为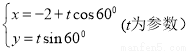 .若C与
.若C与 的交点为P,求点P与点A(-2,0)的距离|PA|.
的交点为P,求点P与点A(-2,0)的距离|PA|.
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高二下学期期末理科数学试卷(解析版) 题型:选择题
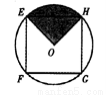
如图,EFGH是以O为圆心,1为半径的圆的内接正方形,将一颗豆子随机地掷到圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形HOE(阴影部分)内”,则P(B|A)=( )
A.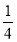 B.
B.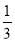 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考理科数学试卷(解析版) 题型:解答题
对于三次函数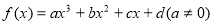 ,定义
,定义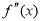 是
是 的导函数
的导函数 的导函数,若方程
的导函数,若方程 有实数解
有实数解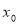 ,则称点
,则称点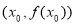 为函数
为函数 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数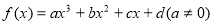 都关于点
都关于点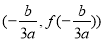 对称:
对称:
②存在三次函数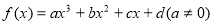 ,若
,若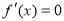 有实数解
有实数解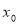 ,则点
,则点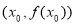 为函数
为函数 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数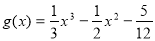 ,则:
,则: 
其中所有正确结论的序号是( ).
A.①②④ B.①②③ C.①③④ D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com