

 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;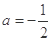 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. ;(Ⅱ)0.
;(Ⅱ)0.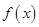 在
在 上为增函数,则它的导函数
上为增函数,则它的导函数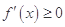 在
在 上恒成立,于是问题转化为不等式恒成立问题,这类问题若方便分离参数一般分离参数,若不方便分离参数,则可从函数自身的单调性解决,但往往会涉及分类讨论,较为麻烦,根据题目特点,本题需要采用第二种方法;(Ⅱ)这是一个由方程有解求参数取值范围(或最值)的问题,这类问题若方便分离参一般可分离参数,转化为求函数的值域问题,若不方便分离参数,则根据函数类型,采用数形结合方法解答,本题适合于第一种方法,但本题分离参数后,若直接求
上恒成立,于是问题转化为不等式恒成立问题,这类问题若方便分离参数一般分离参数,若不方便分离参数,则可从函数自身的单调性解决,但往往会涉及分类讨论,较为麻烦,根据题目特点,本题需要采用第二种方法;(Ⅱ)这是一个由方程有解求参数取值范围(或最值)的问题,这类问题若方便分离参一般可分离参数,转化为求函数的值域问题,若不方便分离参数,则根据函数类型,采用数形结合方法解答,本题适合于第一种方法,但本题分离参数后,若直接求 的最值,则较为困难,比较巧妙的做法是,将问题转化为求
的最值,则较为困难,比较巧妙的做法是,将问题转化为求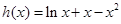 的最值.
的最值.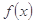 在
在 上为增函数,所以
上为增函数,所以 在
在 上恒成立
上恒成立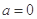 时,
时, 在
在 上恒成立,
上恒成立,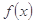 在
在 上为增函数,故
上为增函数,故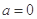 符合题意
符合题意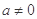 时,由函数
时,由函数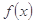 的定义域可知,必须有
的定义域可知,必须有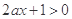 对
对 恒成立,故只能
恒成立,故只能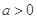 ,所以
,所以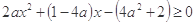 在
在 上恒成立
上恒成立 ,其对称轴为
,其对称轴为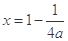 ,因为
,因为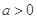 ,所以
,所以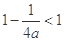 ,要使
,要使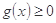 在
在 上恒成立,只要
上恒成立,只要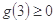 即可,
即可, 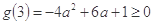 ,所以
,所以 因为
因为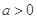 ,所以
,所以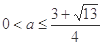 .综上所述,
.综上所述, 的取值范围为
的取值范围为
 时,
时, 可化为
可化为 ,
, 在
在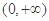 上有解,
上有解,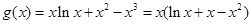 的值域,
的值域,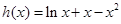 ,
, ,
,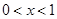 时,
时,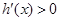 ,
, 在
在 上为增函数,当
上为增函数,当 时,
时,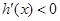 ,
, 在
在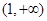 上为减函数,因此
上为减函数,因此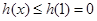 ,
, ,所以
,所以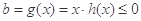 ,即当
,即当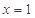 时,
时, 取得最大值0.
取得最大值0.

科目:高中数学 来源:不详 题型:解答题
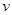 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度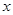 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到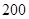 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当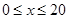 时,车流速度为
时,车流速度为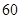 千米/小时.研究表明:当
千米/小时.研究表明:当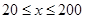 时,车流速度
时,车流速度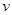 是车流密度
是车流密度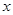 的一次函数.
的一次函数.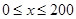 时,求函数
时,求函数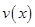 的表达式;
的表达式;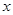 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)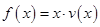 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
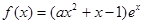 ,其中
,其中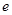 是自然对数的底数,
是自然对数的底数,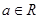 .
.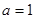 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;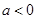 ,求
,求 的单调区间;
的单调区间; ,函数
,函数 的图象与函数
的图象与函数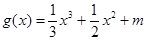 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数 的取值范围.
的取值范围. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com