
一次函数 是
是 上的增函数,
上的增函数, ,已知
,已知 .
.
(1)求 ;
;
(2)若 在
在 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;
(3)当 时,
时, 有最大值
有最大值 ,求实数
,求实数 的值.
的值.
(1)  ;(2)
;(2)  的取值范围为
的取值范围为 ;(3)
;(3)  或
或 .
.
【解析】
试题分析:(1)利用待定系数法设 ,
, ,
, ,解得
,解得 或
或 (不合题意舍去),
(不合题意舍去),
∴ ;
;
(2)由(1)有 ,根据二次函数的性质,当
,根据二次函数的性质,当 在
在 单调递增,则对称轴
单调递增,则对称轴 ,解得
,解得 ;
;
(3)分情况讨论,考虑对称轴的位置,利用单调性求最值,①当 时,即
时,即 时
时
 ,解得
,解得 ,符合题意;②当
,符合题意;②当 时,即
时,即 时
时
 ,解得
,解得 ,符合题意;由①②可得
,符合题意;由①②可得 或
或 .
.
试题解析:(1)∵ 是
是 上的增函数,∴设
上的增函数,∴设 1分
1分

∴ , 3分
, 3分
解得 或
或 (不合题意舍去) 5分
(不合题意舍去) 5分
∴ 6分
6分
(2) 7分
7分
对称轴 ,根据题意可得
,根据题意可得 , 8分
, 8分
解得
∴ 的取值范围为
的取值范围为 9分
9分
(3)①当 时,即
时,即 时
时
 ,解得
,解得 ,符合题意; 11分
,符合题意; 11分
②当 时,即
时,即 时
时
 ,解得
,解得 ,符合题意; 13分
,符合题意; 13分
由①②可得 或
或 14分
14分
考点:本题考查函数的解析式求法,二次函数的单调性和最值性,分类讨论思想.


科目:高中数学 来源:2016届广东实验中学高一一级模块考试数学试卷(解析版) 题型:选择题
给岀四个命题:
(1)若一个角的两边分别平行于另一个角的两边,则这两个角相等;
(2)?,?为两个不同平面,直线a??,直线b??,且a∥?,b∥?,则?∥?;
(3)?,?为两个不同平面,直线m⊥?,m⊥?,则?∥?;
(4)?,?为两个不同平面,直线m∥?,m∥?,则?∥? .
其中正确的是( )
A.(1) B.(2) C.(3) D.(4)
查看答案和解析>>
科目:高中数学 来源:2016届山东省文登市高一上学期期末统考数学试卷(解析版) 题型:选择题
点 是直线
是直线 上动点,
上动点, 是圆
是圆 :
: 的两条切线,
的两条切线, 是切点,若四边形
是切点,若四边形 的最小面积是
的最小面积是 ,则
,则 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届山东省文登市高一上学期期末统考数学试卷(解析版) 题型:选择题
一个几何体的三视图如下图所示,这个几何体可能是一个( )

A.三棱锥 B.底面不规则的四棱锥
C.三棱柱 D.底面为正方形的四棱锥
查看答案和解析>>
科目:高中数学 来源:2016届山东省威海市高一上学期期末考试数学试卷(解析版) 题型:选择题
已知函数 ,若对于任意
,若对于任意 ,当
,当 时,总有
时,总有 ,则区间
,则区间 有可能是( )
有可能是( )
(A) (B)
(B)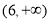 (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2016届宁夏高一上学期期末考试数学试卷(解析版) 题型:填空题
下面给出五个命题:
①已知平面 //平面
//平面 ,
, 是夹在
是夹在 间的线段,若
间的线段,若 //
// ,则
,则 ;
;
② 是异面直线,
是异面直线, 是异面直线,则
是异面直线,则 一定是异面直线;
一定是异面直线;
③三棱锥的四个面可以都是直角三角形。
④平面 //平面
//平面 ,
, ,
, //
// ,则
,则 ;
;
⑤三棱锥中若有两组对棱互相垂直,则第三组对棱也一定互相垂直;
其中正确的命题编号是 (写出所有正确命题的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com