Question

（2012•广州一模）如图所示，在三棱锥P-ABC中，AB=BC=

6

，平面PAC⊥平面ABC，PD⊥AC于点D，AD=1，CD=3，PD=

3

．
（1）证明△PBC为直角三角形；
（2）求直线AP与平面PBC所成角的正弦值．

Answer 1

分析：（1）证明1：先证明PD⊥平面ABC，在△PBC中，可得BC=

6

，PB=

6

，PC=2

3

，从而BC²+PB²=PC²．
证明2：先证明PD⊥平面ABC，再证明BC⊥BD，BC⊥PD，从而可得BC⊥平面PBD．
（2）解法1：过点A作平面PBC的垂线，垂足为H，连PH，则∠APH为直线AP与平面PBC所成的角，利用三棱锥A-PBC与三棱锥P-ABC的体积相等，可求AH的长，在Rt△PAD中，，可求AP的长，从而可求直线AP与平面PBC所成角的正弦值；
解法2：过点D作DM∥AP，设DM∩PC=M，则DM与平面PBC所成的角等于AP与平面PBC所成的角，过点D作DN⊥PB于点N，连接MN，则可得∠DMN为直线DM与平面PBC所成的角，求出DN，DE的长，即可求得直线AP与平面PBC所成角的正弦值；
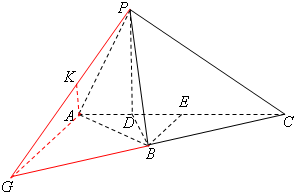
解法3：延长CB至点G，使得BG=BC，连接AG、PG，过点A作AK⊥PG于点K，可证∠APK为直线AP与平面PBC所成的角，计算AG，PG的长，可得直线AP与平面PBC所成角的正弦值为

6

3

；
解法4：建立空间直角坐标系，确定

AP

=(0，1，

3

)，平面PBC的法向量，利用向量的夹角公式，可求直线AP与平面PBC所成角的正弦值．

解答：（1）证明1：因为平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，PD?平面PAC，PD⊥AC，所以PD⊥平面ABC．…（1分）
记AC边上的中点为E，在△ABC中，AB=BC，所以BE⊥AC．
因为AB=BC=

6

，AC=4，所以BE=

BC2-CE2

=

( 6 )2-22

=

2

．…（3分）
因为PD⊥AC，所以△PCD为直角三角形．
因为PD=

3

，CD=3，
所以PC=

PD2+CD2

=

( 3 )2+32

=2

3

．…（4分）
连接BD，在Rt△BDE中，因为BE=

2

，DE=1，
所以BD=

BE2+DE2

=

( 2 )2+12

=

3

．…（5分）
因为PD⊥平面ABC，BD?平面ABC，所以PD⊥BD．
在Rt△PBD中，因为PD=

3

，BD=

3

，
所以PB=

PD2+BD2

=

( 3 )2+( 3 )2

=

6

．…（6分）
在△PBC中，因为BC=

6

，PB=

6

，PC=2

3

，
所以BC²+PB²=PC²．
所以△PBC为直角三角形．…（7分）
证明2：因为平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，PD?平面PAC，PD⊥AC，
所以PD⊥平面ABC．…（1分）
记AC边上的中点为E，在△ABC中，因为AB=BC，所以BE⊥AC．
因为AB=BC=

6

，AC=4，所以BE=

BC2-CE2

=

( 6 )2-22

=

2

．…（3分）
连接BD，在Rt△BDE中，因为∠BED=90°，BE=

2

，DE=1，
所以BD=

BE2+DE2

=

( 2 )2+12

=

3

．…（4分）
在△BCD中，因为CD=3，BC=

6

，BD=

3

，
所以BC²+BD²=CD²，所以BC⊥BD．…（5分）
因为PD⊥平面ABC，BC?平面ABC，
所以BC⊥PD．…（6分）
因为BD∩PD=D，所以BC⊥平面PBD．
因为PB?平面PBD，所以BC⊥PB．
所以△PBC为直角三角形．…（7分）
（2）解法1：过点A作平面PBC的垂线，垂足为H，连PH，则∠APH为直线AP与平面PBC所成的角．…（8分）
由（1）知，△ABC的面积S△ABC=

1

2

×AC×BE=2

2

．…（9分）
因为PD=

3

，所以VP-ABC=

1

3

×S△ABC×PD=

1

3

×2

2

×

3

=

2 6

3

．…（10分）
由（1）知△PBC为直角三角形，BC=

6

，PB=

6

，
所以△PBC的面积S△PBC=

1

2

×BC×PB=

1

2

×

6

×

6

=3．…（11分）
因为三棱锥A-PBC与三棱锥P-ABC的体积相等，即V_A-PBC=V_P-ABC，
即

1

3

×3×AH=

2 6

3

，所以AH=

2 6

3

．…（12分）
在Rt△PAD中，因为PD=

3

，AD=1，
所以AP=

PD2+AD2

=

( 3 )2+12

=2．…（13分）
因为sin∠APH=

AH

AP

=

2 6 3

2

=

6

3

．
所以直线AP与平面PBC所成角的正弦值为

6

3

．…（14分）
解法2：过点D作DM∥AP，设DM∩PC=M，则DM与平面PBC所成的角等于AP与平面PBC所成的角．…（8分）
由（1）知BC⊥PD，BC⊥PB，且PD∩PB=P，所以BC⊥平面PBD．
因为BC?平面PBC，所以平面PBC⊥平面PBD．
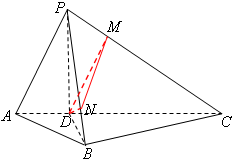
过点D作DN⊥PB于点N，连接MN，则DN⊥平面PBC．
所以∠DMN为直线DM与平面PBC所成的角．…（10分）
在Rt△PAD中，因为PD=

3

，AD=1，
所以AP=

PD2+AD2

=

( 3 )2+12

=2．…（11分）因为DM∥AP，所以

DM

AP

=

CD

CA

，即

DM

2

=

3

4

，所以DM=

3

2

．…（12分）
由（1）知BD=

3

，PB=

6

，且PD=

3

，
所以DN=

PD×BD

PB

=

3 × 3

6

=

6

2

．…（13分）
因为sin∠DMN=

DN

DE

=

6 2

3 2

=

6

3

，
所以直线AP与平面PBC所成角的正弦值为

6

3

．…（14分）
解法3：延长CB至点G，使得BG=BC，连接AG、PG，…（8分）
在△PCG中，PB=BG=BC=

6

，所以∠CPG=90°，即CP⊥PG．
在△PAC中，因为PC=2

3

，PA=2，AC=4，所以PA²+PC²=AC²，
所以CP⊥PA．
因为PA∩PG=P，所以CP⊥平面PAG．…（9分）
过点A作AK⊥PG于点K，
因为AK?平面PAG，所以CP⊥AK．
因为PG∩CP=P，所以AK⊥平面PCG．
所以∠APK为直线AP与平面PBC所成的角．…（11分）
由（1）知，BC⊥PB，所以PG=PC=2

3

．
在△CAG中，点E、B分别为边CA、CG的中点，
所以AG=2BE=2

2

．…（12分）
在△PAG中，PA=2，AG=2

2

，PG=2

3

，
所以PA²+AG²=PG²，即PA⊥AG．…（13分）
因为sin∠APK=

AG

PG

=

2 2

2 3

=

6

3

．
所以直线AP与平面PBC所成角的正弦值为

6

3

．…（14分）
解法4：以点E为坐标原点，以EB，EC所在的直线分别为x轴，y轴建立如图的空间直角坐标系E-xyz，…（8分）
则A（0，-2，0），B(

2

，0，0)，C（0，2，0），P(0，-1，

3

)．
于是