
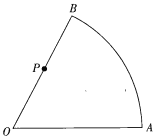
【题目】某学校在一块圆心角为![]() ,半径等于
,半径等于![]() 的扇形空旷地域(如图)组织学生进行野外生存训练,已知在O,A,B处分别有50名,150名,100名学生,现要在道路OB(包括O,B两点)上设置集合地点P,要求所有学生沿最短路径到P点集合,则所有学生行进的最短总路程为_____________
的扇形空旷地域(如图)组织学生进行野外生存训练,已知在O,A,B处分别有50名,150名,100名学生,现要在道路OB(包括O,B两点)上设置集合地点P,要求所有学生沿最短路径到P点集合,则所有学生行进的最短总路程为_____________![]() .
.
科目:高中数学 来源: 题型:
【题目】在正三棱锥P﹣ABC中,PA,PB,PC两两垂直,![]() ,点E在线段AB上,且AE=2EB,过点E作该正三棱锥外接球的截面,则所得截面圆面积的最小值是( )
,点E在线段AB上,且AE=2EB,过点E作该正三棱锥外接球的截面,则所得截面圆面积的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() :
:![]() 上的点按坐标变换
上的点按坐标变换![]() ,得到曲线
,得到曲线![]() ,
,![]() 为
为![]() 与
与![]() 轴负半轴的交点,经过点
轴负半轴的交点,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,与曲线
,与曲线![]() 的交点分别为
的交点分别为![]() ,
,![]() (点
(点![]() 在第二象限).
在第二象限).
(Ⅰ)写出曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从洛阳的高中生中,随机抽取了55人,从上海的高中生中随机抽取了45人进行答题.洛阳高中生答题情况是:选择家的占![]() 、选择朋友聚集的地方的占
、选择朋友聚集的地方的占![]() 、选择个人空间的占
、选择个人空间的占![]() .上海高中生答题情况是:选择朋友聚集的地方的占
.上海高中生答题情况是:选择朋友聚集的地方的占![]() 、选择家的占
、选择家的占![]() 、选择个人空间的占
、选择个人空间的占![]() .
.
(1)请根据以上调查结果将下面![]() 列联表补充完整,并判断能否有
列联表补充完整,并判断能否有![]() 的把握认为“恋家(在家里感到最幸福)”与城市有关:
的把握认为“恋家(在家里感到最幸福)”与城市有关:
在家里最幸福 | 在其它场所最幸福 | 合计 | |
洛阳高中生 | |||
上海高中生 | |||
合计 |
(2) 从被调查的不“恋家”的上海学生中,用分层抽样的方法选出4人接受进一步调查,从被选出的4 人中随机抽取2人到洛阳交流学习,求这2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() d.
d.

查看答案和解析>>
科目:高中数学 来源: 题型:
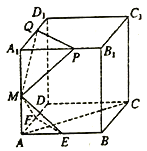
【题目】如图,已知在棱长为1的正方体![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() ,
,![]() 的中点,又
的中点,又![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上,且
上,且![]() .设平面
.设平面![]() 平面
平面![]() ,现有下列结论:
,现有下列结论:
①![]() 平面
平面![]() ;
;
②![]() ;
;
③直线![]() 与平面
与平面![]() 不垂直;
不垂直;
④当![]() 变化时,
变化时,![]() 不是定直线.
不是定直线.
其中不成立的结论是______.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 为曲线
为曲线![]() 上的点,
上的点,![]() ,垂足为
,垂足为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种昆虫的日产卵数和时间变化有关,现收集了该昆虫第1天到第5天的日产卵数据:
第x天 | 1 | 2 | 3 | 4 | 5 |
日产卵数y(个) | 6 | 12 | 25 | 49 | 95 |
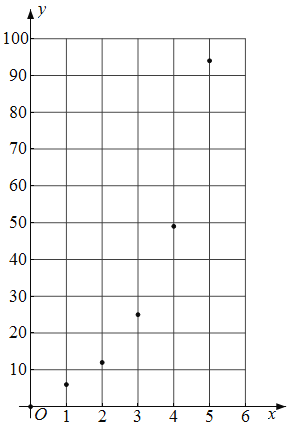
对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
|
|
|
|
15 | 55 | 15.94 | 54.75 |
(1)根据散点图,利用计算机模拟出该种昆虫日产卵数y关于x的回归方程为![]() (其中e为自然对数的底数),求实数a,b的值(精确到0.1);
(其中e为自然对数的底数),求实数a,b的值(精确到0.1);
(2)根据某项指标测定,若日产卵数在区间(e6,e8)上的时段为优质产卵期,利用(1)的结论,估计在第6天到第10天中任取两天,其中恰有1天为优质产卵期的概率.
附:对于一组数据(v1,μ1),(v2,μ2),…,(vn,μn),其回归直线的斜率和截距的最小二乘估计分别为![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的标准方程是
的标准方程是![]() ,设
,设![]() 是椭圆
是椭圆![]() 的左焦点,
的左焦点,![]() 为直线
为直线![]() 上任意一点,过
上任意一点,过![]() 做
做![]() 的垂线交椭圆
的垂线交椭圆![]() 于点
于点![]() ,
,![]() .
.
(1)证明:线段![]() 平分线段
平分线段![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
(2)当![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com