
【题目】在正三棱锥P﹣ABC中,PA,PB,PC两两垂直,![]() ,点E在线段AB上,且AE=2EB,过点E作该正三棱锥外接球的截面,则所得截面圆面积的最小值是( )
,点E在线段AB上,且AE=2EB,过点E作该正三棱锥外接球的截面,则所得截面圆面积的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
构造以PA,PB,PC为棱长的正方体PADB﹣CFGH,且该正方体棱长为![]() ,以B为原点,BP为x轴,BD为y轴,BH为z轴,建立空间直角坐标系,则该正三棱锥外接球球心为AH中点O,半径为R
,以B为原点,BP为x轴,BD为y轴,BH为z轴,建立空间直角坐标系,则该正三棱锥外接球球心为AH中点O,半径为R![]() ,求出EO
,求出EO![]() ,当所得截面圆面积取最小值时截面圆的圆心为E,从而当所得截面圆面积取最小值时截面圆的半径为r
,当所得截面圆面积取最小值时截面圆的圆心为E,从而当所得截面圆面积取最小值时截面圆的半径为r![]() ,由此能求出所得截面圆面积的最小值.
,由此能求出所得截面圆面积的最小值.
∵在正三棱锥P﹣ABC中,PA,PB,PC两两垂直,![]() ,
,
∴构造以PA,PB,PC为棱长的正方体PADB﹣CFGH,且该正方体棱长为![]() ,
,
以B为原点,BP为x轴,BD为y轴,BH为z轴,建立空间直角坐标系,
则该正三棱锥外接球球心为AH中点O,半径为R![]() ,
,
∵点E在线段AB上,且AE=2EB,
∴E(![]() ,
,![]() ,0),O(
,0),O(![]() ),
),
EO![]() ,
,
过点E作该正三棱锥外接球的截面,当所得截面圆面积取最小值时截面圆的圆心为E,
∴当所得截面圆面积取最小值时截面圆的半径为:
r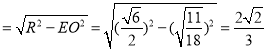 ,
,
∴过点E作该正三棱锥外接球的截面,
则所得截面圆面积的最小值为S=πr2![]() .
.
故选:A.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为
,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)经过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,试证明:直线
,试证明:直线![]() 与
与![]() 轴的交点
轴的交点![]() 为一个定点,且
为一个定点,且![]() (
(![]() 为原点).
为原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为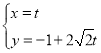 (
(![]() 为参数). 以
为参数). 以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求
,求![]() ;
;
(2)若点![]() 是曲线
是曲线![]() 上不同于
上不同于![]() 的动点,求
的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的直线l:
的直线l:![]() 与抛物线E:
与抛物线E:![]() (
(![]() )交于B,C两点,且A为线段
)交于B,C两点,且A为线段![]() 的中点.
的中点.
(1)求抛物线E的方程;
(2)已知直线![]() :
:![]() 与直线l平行,过直线
与直线l平行,过直线![]() 上任意一点P作抛物线E的两条切线,切点分别为M,N,是否存在这样的实数m,使得直线
上任意一点P作抛物线E的两条切线,切点分别为M,N,是否存在这样的实数m,使得直线![]() 恒过定点A?若存在,求出m的值;若不存在,说明理由.
恒过定点A?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的方程为![]() .在以原点O为极点,x轴正半轴为极轴的极坐标系中,P的极坐标为
.在以原点O为极点,x轴正半轴为极轴的极坐标系中,P的极坐标为![]() ,直线l过点P.
,直线l过点P.
(1)若直线l与OP垂直,求直线l的直角标方程:
(2)若直线l与曲线C交于A,B两点,且![]() ,求直线l的倾斜角.
,求直线l的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离。

查看答案和解析>>
科目:高中数学 来源: 题型:
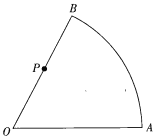
【题目】某学校在一块圆心角为![]() ,半径等于
,半径等于![]() 的扇形空旷地域(如图)组织学生进行野外生存训练,已知在O,A,B处分别有50名,150名,100名学生,现要在道路OB(包括O,B两点)上设置集合地点P,要求所有学生沿最短路径到P点集合,则所有学生行进的最短总路程为_____________
的扇形空旷地域(如图)组织学生进行野外生存训练,已知在O,A,B处分别有50名,150名,100名学生,现要在道路OB(包括O,B两点)上设置集合地点P,要求所有学生沿最短路径到P点集合,则所有学生行进的最短总路程为_____________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天或每月行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
根据折线图,下列结论正确的是( )
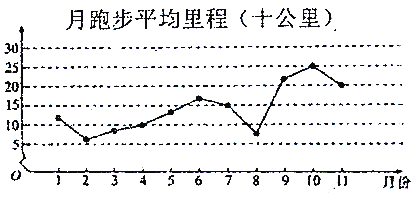
A. 月跑步平均里程的中位数为![]() 月份对应的里程数
月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在![]() 、
、![]() 月
月
D. ![]() 月至
月至![]() 月的月跑步平均里程相对于
月的月跑步平均里程相对于![]() 月至
月至![]() 月,波动性更小,变化比较平稳
月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com