
����Ŀ�����ں���f��x��=sin��x��![]() ��sin��x+
��sin��x+![]() �������������⣺
�������������⣺
�ٴ˺������Ի�Ϊf��x��=��![]() sin��2x+
sin��2x+![]() ����
����
�ں���f��x������С�������ǦУ���ͼ���һ���Գ������ǣ�![]() �� 0����
�� 0����
�ۺ���f��x������СֵΪ��![]() �� ��ͼ���һ���Գ�����x=
�� ��ͼ���һ���Գ�����x=![]() ��
��
�ܺ���f��x����ͼ������ƽ��![]() ����λ��õ��ĺ�����ż������
����λ��õ��ĺ�����ż������
�ݺ���f��x�������䣨��![]() �� 0�����Ǽ�������
�� 0�����Ǽ�������
����������ȷ���������Ÿ����ǣ�������
A.2
B.3
C.4
D.5
���𰸡�C
����������f��x��=sin��x��![]() ��sin��x+
��sin��x+![]() ��=��
��=��![]() [cos��2x+
[cos��2x+![]() ����cos����
����cos����![]() ��]=��
��]=��![]() cos��2x+
cos��2x+![]() ��=��
��=��![]() sin[
sin[![]() ����2x+
����2x+![]() ��]=��
��]=��![]() sin��
sin��![]() ��2x��=��
��2x��=��![]() sin[����
sin[����![]() ��2x��]=��
��2x��]=��![]() sin��2x+
sin��2x+![]() ��������ȷ��
��������ȷ��
���ɢٵ�f��x��=��![]() cos��2x+
cos��2x+![]() �����Ӷ����T=
�����Ӷ����T=![]() =�У���2x+
=����2x+![]() =k
=k![]() +
+![]() �ɽ�ã�x=
�ɽ�ã�x=![]() +
+![]() �� k��Z����k=0ʱ����
�� k��Z����k=0ʱ����![]() �� 0����һ���Գ����ģ�����ȷ��
�� 0����һ���Գ����ģ�����ȷ��
���ɢٵ�f��x��=��![]() cos��2x+
cos��2x+![]() ������2x+
������2x+![]() =k�пɽ�ã�x=
=k�пɽ�ã�x=![]() -
-![]() k��Z����k=1ʱ��ͼ���һ���Գ�����x=
k��Z����k=1ʱ��ͼ���һ���Գ�����x=![]() �� ����f��x������СֵΪ��
�� ����f��x������СֵΪ��![]() �� ����ȷ��
�� ����ȷ��
�ܺ���f��x����ͼ������ƽ��![]() ����λ��õ��ĺ���Ϊf��x��
����λ��õ��ĺ���Ϊf��x��![]() ��=��
��=��![]() cos[2��x��
cos[2��x��![]() ��+
��+![]() ]=��
]=��![]() cos[2x��
cos[2x��![]() +
+![]() ]=��
]=��![]() cos2x����ż����������ȷ��
cos2x����ż����������ȷ��
���ɢٵ�f��x��=��![]() cos��2x+
cos��2x+![]() ������2k����2x+
������2k�Щ��С�2x+![]() ��2�У��ɽ�ã�
��2�У��ɽ�ã�![]() -
-![]() ��x��k
��x��k![]() -
-![]() �� k��Z������k=0ʱ����f��x�������䣨��
�� k��Z������k=0ʱ����f��x�������䣨��![]() �� ��
�� ��![]() �����Ǽ��������ʲ���ȷ��
�����Ǽ��������ʲ���ȷ��
���Ͽɵã�������ȷ���������Ÿ�����4����
��ѡ��C��
�����㾫����������Ĺؼ������������Ǻ����Ļ����Ͳʽ�����֪ʶ���������Ǻ����Ļ����Ͳʽ��![]() ;
;![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=ex �� g��x��=lnx����f��t��=g��s������s��tȡ����Сֵʱ��f��t�����������ǣ� ��
A.��ln2��1��
B.�� ![]() ��ln2��
��ln2��
C.�� ![]() ��
�� ![]() ��
��
D.�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��С�����εı߳�Ϊ1����ʵ��������ij�����������ͼ����ö�����ĸ����У���������ǣ� �� 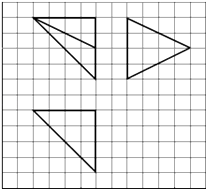
A.8
B.![]()
C.12
D.16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�a��b��c�ֱ�Ϊ�ڽ�A��B��C�ĶԱߣ���bsin2C=csinB��
��1�����C��
��2���� ![]() ����sinA��ֵ��
����sinA��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��C������ֱ�Ϊ���� ![]() ��0������
��0������ ![]() ��0������m��n����G��O�䣬H�ֱ�Ϊ��ABC�����ģ����ģ����ģ�
��0������m��n����G��O�䣬H�ֱ�Ϊ��ABC�����ģ����ģ����ģ� 
��1��д������G�����ꣻ
��2��������O�䣬����H�����ꣻ
��3����֤��G��H��O�����㹲�ߣ�������|GH|=2|OG��|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��=cos����x+�գ����أ�0��|��|�� ![]() ����ͼ���ϵ�ÿһ��������겻�䣬����������Ϊԭ����һ�룬�ٽ�ͼ������ƽ��
����ͼ���ϵ�ÿһ��������겻�䣬����������Ϊԭ����һ�룬�ٽ�ͼ������ƽ�� ![]() ����λ���ȵõ�����y=sinx��ͼ��
����λ���ȵõ�����y=sinx��ͼ��
��1��ֱ��д��f��x���ı���ʽ�������f��x����[0����]�ϵ�ֵ��
��2�����f��x����[0����]�ϵĵ������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
��
�������f��x����x=0��ȡ�ü�ֵ����k��ֵ��
��������f��x���ĵ������䣻
��III����k=0ʱ������A��0��t�����ں�������f��x�������ߣ���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����a1=2��an+1=2an��1��
����������{an}��ͨ�ʽ��
������bn=n��an��1����������{bn}��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�CD�ǡ�ACB��ƽ���ߣ���ACD�����Բ��BC�ڵ�E��AB=2AC��
��1����֤��BE=2AD��
��2������AC=1��BC=2ʱ����AD�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com