
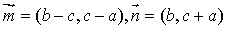 ,若
,若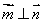 ,则角A的大小为( )
,则角A的大小为( )A.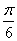 | B.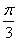 | C.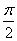 | D.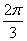 |
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:不详 题型:解答题
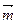 ="(a-b,c),"
="(a-b,c)," 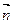 =(a-c,a+b),且
=(a-c,a+b),且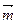 与
与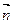 共线。
共线。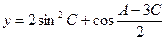 ,求y的最大值及此时∠C的大小。
,求y的最大值及此时∠C的大小。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
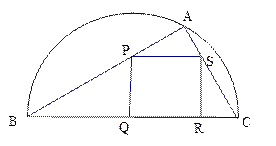 (本小题满分14分)如下图,某小区准备绿化一块直径为
(本小题满分14分)如下图,某小区准备绿化一块直径为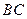 的半圆形空地,
的半圆形空地,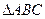 的内接正方形
的内接正方形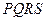 为一水池,
为一水池,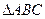 外的地方种草,其余地方种花.若
外的地方种草,其余地方种花.若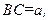
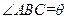 ,设
,设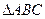 的面积为
的面积为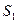 ,正方形
,正方形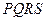 的面积为
的面积为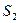 ,将比值
,将比值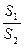 称为“规划合理度”.?(Ⅰ) 试用
称为“规划合理度”.?(Ⅰ) 试用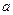 ,
,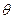 表示
表示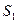 和
和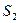 ;??(Ⅱ) 若
;??(Ⅱ) 若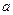 为定值,当
为定值,当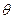 为何值时,“规划合理度”最小?并求出这个最小值.
为何值时,“规划合理度”最小?并求出这个最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
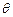 的余弦值为
的余弦值为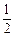 . (1)求角B的大小; (2)求sinA + sinC的取值范围.
. (1)求角B的大小; (2)求sinA + sinC的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com