
 如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=
如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=| 2 |
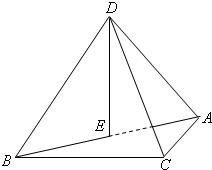 解:(Ⅰ)取AB的中点E,连接DE,CE,
解:(Ⅰ)取AB的中点E,连接DE,CE,| 3 |
| DE2+EC2 |


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
 12、如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形.
12、如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )
如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com