练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    正方体中，点分别在线段上，且 ．以下结论：①；②；③MN//平面；④MN与异面；⑤MN⊥平面．其中有可能成立的结论的个数为（    ）
    A．5B．4 C．3D．2
    A

     
    作垂足是
    则是平行四边形；

    当分别是线段的中点时，分别是的中点；此时
    则
    当在点时，在点此时与异面；
    当分别是线段的中点时，故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

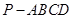    （本小题满分12分）如图四棱锥的底面是正方形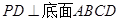，，点E在棱PB上，O为AC与BD的交点。
    （1）求证：平面；
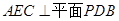    （2）当E为PB中点时，求证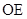：//平面PDA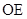，//平面PDC。
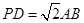    （3）当且E为PB的中点时，求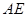与平面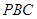所成的角的大小。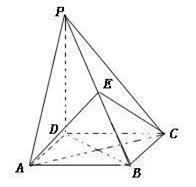

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知a、b为两条不同的直线，α、β为两个不同的平面，
    且a⊥α，b⊥β，则下列命题中为假命题的是
    A．若a∥b，则α∥β
    B．若α⊥β，则a⊥b
    C．若a，b相交，则α，β相交
    D．若α，β相交，则a，b相交

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分14分）在直三棱柱ABC—A1B1C1中，∠ACB=90°，AC=BC=AA1=1，D、E分别为棱AB、BC的中点，M为棱AA1上的点。
      
    （1）证明：A1B1⊥C1D；
    （2）当的大小。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是地面边长的倍，P为侧棱SD上的点。
    （1）求证：AC⊥SD；
    （2）若SD⊥平面PAC，求二面角P-AC-D的大小
    （3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC。若存在，求SE：EC的值；若不存在，试说明理由。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    判断下列命题，正确的个数为（   　）
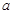    ①直线与平面没有公共点，则；
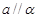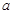    ②直线平行于平面内的一条直线，则；
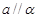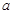    ③直线与平面内的无数条直线平行，则；
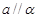    ④平面内的两条直线分别平行于平面，则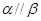
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    如图，四边形是直角梯形，∠＝90°，∥，＝1，＝2，又＝1，∠＝120°，⊥，直线与直线所成的角为60°.
    （1）求证：平面⊥平面；
    （2）求三棱锥的体积；

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图，正方体中，分别为BC, CC1中点，
    则异面直线与所成角的大小为
                                 

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在空间四边形ABCD各边AB、BC、CD、DA上分别取E、F、G、H四点，如果EF、GH相交于点P，那么(    )
    A．点P必在直线AC上 B.点P必在直线BD上
    C．点P必在平面DBC内              D.点P必在平面ABC外

    查看答案和解析>>

    同步练习册答案