
分析 (1)依题意$\frac{c}{a}=\frac{{\sqrt{6}}}{3},2ab=4\sqrt{3}$,解得a2,b2的值,进而可得椭圆方程;
(2)联立方程组$\left\{{\begin{array}{l}{y=k(x-2)}\\{\frac{x^2}{6}+\frac{y^2}{2}=1}\end{array}}\right.$,结合韦达定理,及△ABP为正三角形时,$|{MP}|=\frac{{\sqrt{3}}}{2}|{AB}|$,求出k值,可得直线l的方程.
解答 解:(1)依题意$\frac{c}{a}=\frac{{\sqrt{6}}}{3},2ab=4\sqrt{3}$,
可得$\frac{{{a^2}-{b^2}}}{a^2}=\frac{2}{3},{a^2}{b^2}=12$…(2分)
得a2=6,b2=2.
所以所求椭圆方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$…(5分)
(2)直线l的方程为y=k(x-2),联立方程组$\left\{{\begin{array}{l}{y=k(x-2)}\\{\frac{x^2}{6}+\frac{y^2}{2}=1}\end{array}}\right.$,
消去y并整理得(3k2+1)x2-12k2x+12k2-6=0.
设A(x1,y1),B(x2,y2),得${x_1}+{x_2}=\frac{{12{k^2}}}{{3{k^2}+1}}$,${x_1}{x_2}=\frac{{12{k^2}-6}}{{3{k^2}+1}}$,
所以$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\frac{{2\sqrt{6}({k^2}+1)}}{{3{k^2}+1}}$…(7分)
设AB的中点M(x0,y0),得${x_0}=\frac{{6{k^2}}}{{3{k^2}+1}}$,${y_0}=-\frac{2k}{{3{k^2}+1}}$…(8分)
得直线MP的斜率为$-\frac{1}{k}$,又xp=3,
所以$|{MP}|=\sqrt{1+\frac{1}{k^2}}•|{{x_0}-{x_P}}|=\sqrt{\frac{{{k^2}+1}}{k^2}}•\frac{{3({k^2}+1)}}{{(3{k^2}+1)}}$…(10分)
当△ABP为正三角形时,$|{MP}|=\frac{{\sqrt{3}}}{2}|{AB}|$,
即$\sqrt{\frac{{{k^2}+1}}{k^2}}•\frac{{3({k^2}+1)}}{{(3{k^2}+1)}}=\frac{{\sqrt{3}}}{2}•\frac{{2\sqrt{6}({k^2}+1)}}{{3{k^2}+1}}$.
解得k=±1.即直线l的方程为x-y-2=0或x+y-2=0…(12分)
点评 本题考查的知识点是椭圆的标准方程,直线与圆锥曲线的综合应用,难度中档.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
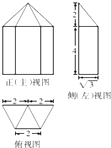 一个几何体的三视图如图所示,则该几何体的体积为( )
一个几何体的三视图如图所示,则该几何体的体积为( )| A. | 14$\sqrt{3}$ | B. | 10$\sqrt{3}$ | C. | 12 | D. | 16$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | 0 | C. | -$\frac{1}{2}$或0 | D. | 0或7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com