
【题目】已知函数![]()
![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)讨论函数![]() 零点的个数.
零点的个数.
【答案】(1)见解析;(2)当![]() 或
或![]() 时,函数有一个零点,当
时,函数有一个零点,当![]() 且
且![]() 时,函数有两个零点.
时,函数有两个零点.
【解析】试题分析:
(1)分类讨论:当![]() 时,
时,![]() 的定义域为
的定义域为![]() ,
,![]() ,令
,令![]() 得:
得:![]() ,
,![]() ,则
,则![]() 的单调递增区间为
的单调递增区间为![]() .当
.当![]() 时,
时,![]() 的定义域为
的定义域为![]() ,
,![]() ,当
,当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,当
,当![]() 时,
时,![]()
![]() .
.![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() .
.
(2)由(1)知当![]() 时,
时,![]() 只有一个零点
只有一个零点![]() ,
,
当![]() 时,
时,![]() 在
在![]() 处取极大值,
处取极大值,![]() 处取极小值.
处取极小值.![]() ,
,![]() ,即
,即![]() 时,函数
时,函数![]() 只有一个零点
只有一个零点![]() ,
,
当![]() 时,令
时,令![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,![]() (当且仅当
(当且仅当![]() 时,等号成立),则:
时,等号成立),则:
![]() 时,
时,![]() 在
在![]() 有两个零点.
有两个零点.![]() 时,
时,![]() 在
在![]() 有两个零点.
有两个零点.![]() 时,函数在
时,函数在![]() 有一个零点.故当
有一个零点.故当![]() 或
或![]() 时,函数有一个零点,当
时,函数有一个零点,当![]() 且
且![]() 时,函数有两个零点.
时,函数有两个零点.
试题解析:
(1)当![]() 时,
时,![]() 的定义域为
的定义域为![]() ,
,
![]()
![]() ,令
,令![]() 得:
得:
![]() ,
,![]() ,
,
∴![]() 的单调递增区间为
的单调递增区间为![]() .
.
当![]() 时,
时,![]() 的定义域为
的定义域为![]() ,
,![]()
![]() ,
,
当![]() 即
即![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,
,
当![]() ,即
,即![]() 时,
时,![]()
![]() .
.
![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() .
.
(2)由(1)知当![]() 时,
时,![]() 在
在![]() 内单调递增,
内单调递增,![]() ,
,
故![]() 只有一个零点
只有一个零点![]() ,
,
当![]() 时,
时,![]() 在
在![]() 处取极大值,
处取极大值,![]() 处取极小值.
处取极小值.
由![]() 知
知![]() ,而
,而![]() ,则
,则![]() ,
,
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴当![]() 时,函数
时,函数![]() 只有一个零点
只有一个零点![]() ,
,
当![]() 时,
时,
令![]() ,
,
![]() ,
,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() ,∴
,∴![]() (当且仅当
(当且仅当![]() 时,等号成立),
时,等号成立),
i)![]() 时,
时,
![]() ,
,![]() ,
,![]() ,
,
由(1)函数单调性知,![]() ,所以函数在
,所以函数在![]() 存在零点,
存在零点,
∴![]() 在
在![]() 有两个零点.
有两个零点.
ii)![]() 时,
时,
![]() ,
,![]() ,
,![]() ,
,
同理可得函数在![]() 存在零点,
存在零点,
∴![]() 在
在![]() 有两个零点.
有两个零点.
iii)![]() 时,
时,
![]() ,函数在
,函数在![]() 有一个零点.
有一个零点.
综上所述:
当![]() 或
或![]() 时,函数有一个零点,
时,函数有一个零点,
当![]() 且
且![]() 时,函数有两个零点.
时,函数有两个零点.


科目:高中数学 来源: 题型:
【题目】最近,“百万英雄”,“冲顶大会”等一些闯关答题类游戏风靡全国,既能答题,又能学知识,还能挣奖金。若某闯关答题一轮共有4类题型,选手从前往后逐类回答,若中途回答错误,立马淘汰只能观战;若能坚持到4类题型全部回答正确,就能分得现金并获得一枚复活币。每一轮闯关答题顺序为:1.文史常识类;2.数理常识类;3.生活常识类;4.影视艺术常识类,现从全省高中生中调查了100位同学的答题情况统计如下表:

(Ⅰ)现用样本的数据特征估算整体的数据特征,从全省高中生挑选4位同学,记![]() 为4位同学获得奖金的总人数,求
为4位同学获得奖金的总人数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若王同学某轮闯关获得的复活币,系统会在下一轮游戏中自动使用,即下一轮重新进行闯关答题时,若王同学在某一类题型中回答错误,自动复活一次,视为答对该类题型。请问:仍用样本的数据特征估算王同学的数据特征,那么王同学在获得复活币的下一轮答题游戏中能够最终获得奖金的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的下顶点为
的下顶点为![]() ,右顶点为
,右顶点为![]() ,离心率
,离心率![]() ,抛物线
,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线
是抛物线![]() 上一点,抛物线
上一点,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,且
,且![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)若![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,墙上有一壁画,最高点![]() 离地面4米,最低点
离地面4米,最低点![]() 离地面2米,观察者从距离墙
离地面2米,观察者从距离墙![]() 米,离地面高
米,离地面高![]() 米的
米的![]() 处观赏该壁画,设观赏视角
处观赏该壁画,设观赏视角![]()
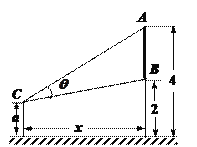
(1)若![]() 问:观察者离墙多远时,视角
问:观察者离墙多远时,视角![]() 最大?
最大?
(2)若![]() 当
当![]() 变化时,求
变化时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角三角形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一个动点,且
上一个动点,且![]() ,如图所示,沿
,如图所示,沿![]() 将
将![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
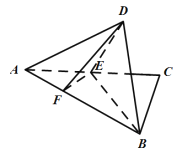
(1)当![]() 时,证明:
时,证明:![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 上的任一点到焦点的距离最大值为3,离心率为
上的任一点到焦点的距离最大值为3,离心率为![]() ,
,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为曲线
为曲线![]() 上两点,
上两点, ![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com